2

I'm new at classical mechanics but the text book says there is the torque in the spinning top which generated only by gravitation. It is hard to explain the situation, I've add the link.

http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/toppre.gif

There is no rotation axis between $r$ (length between the point and center of mass) and $F$ (gravitation), and I don't clearly understand the procession of the torque.

I think the precession of the spinning top is generated by the friction between the surface of the top (close with the point) and ground.

http://www2.picturepush.com/photo/a/13200825/640/13200825.png

Qmechanic
  • 220,844
user25265
  • 21

1 Answers1

-1

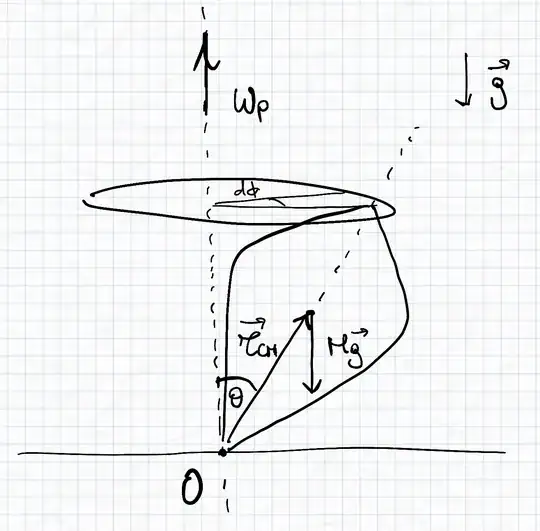Force that count when calculating <span class=$\vec{M}^{e}_{O}$" />

$$\vec{M}^{(e)}_{O}=I\vec{\alpha}=I\frac{d\vec{\omega}}{dt}=\vec{r}_{cm}\times M\vec{g}$$ $$d\vec{\omega}=\frac{\vec{r}_{cm}\times M\vec{g}}{I}dt$$ Now $|r_{cm}\times M \vec{g}|=cost$ , if the foothold is stopped, so $|d\vec{\omega}|$ will be, but because $\vec{M}^{(e)}_{O}\neq 0$ so the direction of $\omega$ has to change $$d\omega=\omega_{spin. top}\sin(\theta)d\phi=\frac{r_{cm}Mg}{I}sin(\theta)dt$$ $$\Rightarrow \vec{\omega_{p}}=\frac{d\phi}{dt}=\frac{r_{cm}Mg}{I\omega_{s.t.}}$$ And thats the only thing you need right there, $$\omega_{p} \propto r_{cm}Mg \qquad \omega_{p}\propto \frac{1}{I\omega_{s.t.}}$$ You can verify this whit small experiments changing spinning top that have different parameters and you can see this proportion, so no it's not because of the friction, the friction only make it so the precession is around an axis passing trough O perpendicular to the ground. If wasn't there friction de precession would have been around an axis passing trough the center of mass , also perpendicolar to the ground

tara
  • 32