3

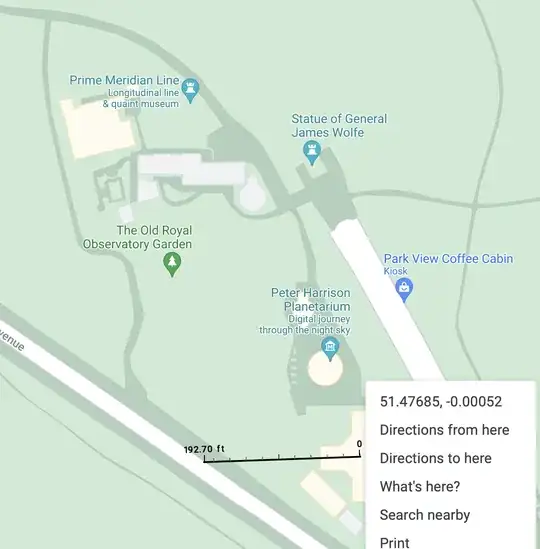
I'm trying to calculate the distance between the WGS84 meridian at 51°28′40.1″N 0°0′5.3″W and the actual prime meridian at 51°28′40.1″N 0°0′0″W in feet. Wiki claims the two points are 5.3'' from each other. My calculation below results in 334 feet and this differs from Wiki's answer of 336.21 feet. I looked at Google maps and used the measure feature, after which I measured 190 feet between both coordinates and this is pictured.

Does anyone know how to correctly calculate this and why the differences between Google, Wiki and my calculation?

$1^\circ = 60′ = 60\,\text{nm} = 69\,\text{mi}$

$1′ = 60″ = 1\,\text{nm} = 1.15\,\text{mi}$

$1″ = 60″′ = 1/60\,\text{nm} = 101.2\,\text{feet}$

$5.3'' \cdot 101.2\,\text{feet} * cos(51.47°) = 334\,\text{feet}$

notaorb
  • 135

2 Answers2

2

You have used the simple rule $$1' = 1\ \text{nm}.$$ This rule is correct for distances in north-south direction. But for distances in west-east direction it is not so simple.

You need to consider the fact that neighboring meridians don't have a constant distance. (Just look at a globe to understand this.) Instead, the meridians get closer and closer to each other, when walking away from the equator towards the north or south pole. At the equator you have $$1' = 1\ \text{nm}.$$ But going away from the equator the correct rule for west-east distances becomes $$1' = \cos(\phi)\cdot 1\ \text{nm}$$ where $\phi$ is the geographical latitude. In your case you have $\phi=51.47°$, and hence $\cos(\phi)=0.6228$.

Thomas Fritsch
  • 42,352
1

The correct answer is 335.573739 feet.

The easiest way to do this is convert lat, lon, height to ECEF and compute the cartesian distance. I just posted the formula here (Actual astronomic latitude (direction of gravity) does not match calculations taking into account centrifugal force of earth).

Of course, that is "as the neutrino flies" and doesn't follow the surface of the Earth. At this distance, the difference is micron tiny.

A more accurate method is to place a locally tangent sphere on one of the points and then project the other onto the sphere, you then get an arc length between them. It gives the same answer to within 1 micron. For instance, if you place the locally tangent sphere at the 1st point, and put the second point on the sphere, you find that it sits at a bearing of 89.9994209 (slightly north of due East), and at a distance of 102.281619 meters, and 0.001028 meters north of great circle pointing due east, with an elevation of 0.9 nanometers (sphere's aren't ellipsoids, but if you use locally Cartesian coordinates, the elevation is -0.8 millimeters, so the sphere is a much better approximation).

An iterative solutions called Vincenty's formula (https://en.wikipedia.org/wiki/Vincenty%27s_formulae) also works.

The 336.5' number is wrong...probably uses the spherical solution.

btw: I used a height for Greenwich of 84.7 meters.

JEB
  • 42,131