Why falling body do not reach Schwarzschild radius in coordinate time but do in proper time?

Question

I do still not really understand the solution for a radially falling body in the Schwarzschild metric:

One the one hand, in terms of proper time $\tau$ the equation of motion can be solved and gives a solution $r(\tau)$ for $r\ge 0$. The body crosses Schwarzschild radius $r_s$ without any problems and the solution is valid also for $r\le r_s$.

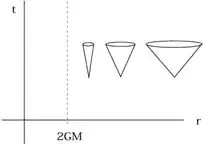
On the other hand, the same calculation, carried out in coordinate time t shows, that the particle is never reaching $r_s$ in finite time.

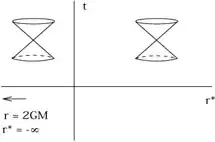
The body definitely crosses the Schwarzschild boundary (although is cannot be proven, because nobody can come back), but why is there no solution for $r\le r_s$? What is the deeper reason, that this region is not mapped by using t? I would expect, that a switch to a new coordinate system maps a point into another unique point. For points inside $r_s$ this seems to be not possible anymore, but, on the other hand, I can easily mark an inside point in the t-r-Diagram and the Schwarzschild Metric is, from its definition, not restricted to $r>r_s$.

I know, that its an artifact due to geometry, but how can it be, that the mapping of inside points between the two coordinate systems fails? Naively speaking, there should be a solution also for the region within Schwarzschild radius because moving astronauts COULD get there and make a meeting. This Meeting, taken as a real event is not visible in the t-r- coordinates. Thinking about that makes me crazy...

Answer 1

The causal structure, defined by light cones can be shown in t-r plane. The slope of the cones given by

\begin{equation}\tag{1} \frac{dt}{dr} = \pm \frac{1}{(1-\frac{r_S}{r})} \end{equation}

increases to infinity for $r\rightarrow r_S$. (first picture below) Hence light rays asymptotically 'reaches' Schwarzschild radius in this coordinate system. The idea of tortoise coordinate is to make $\frac{dt}{dr}$ smaller. Just by integrating (1), we get $r^* = r+r_S \text{ln}(\frac{r}{r_S}-1)+\text{const}$. We can now map $r < r_S$ using tortoise coordinates ($t,r^*$) in which Schwarzschild metric beomes,

\begin{equation} ds^2 = -(1-\frac{r_S}{r})(dt^2 + dr^{*2}) + r^2d\Omega^2) \end{equation}

(because $dr^* = dr/(1-\frac{r_S}{r}))$

Now $dt/dr^*$ is a constant hence we have light cones which are not asymptotic in $t-r^*$ plane (second picture).

The proper time and coordinate time can be related (from geodesic equation) as,

\begin{equation}\tag{2} \frac{d\tau}{dt} = (1-\frac{r_S}{r})^{1/2} \end{equation} Hence, distant observer (named B) will observe light coming from infalling observer (name him A), red shifted by (one over) this factor (and also we cannot define once $r<r_S$ - physically A appears not only to be still but gets reddened and hence eventually dimmer to B).

A reaches $r_S$ in finite proper time but for B at rest, this would take infinite time. In other words, $r_S$ forms the Cauchy Horizon beyond which we have unique geodesics but within it, is a singularity (which does not belong to the Lorentzian manifold) with no future null-like geodesics.

So from (2) it is clear that, even though, A crosses $r_S$, B cannot see this event. Even though A can hold meeting inside the Horizon, B will never know of it. Is there a transformation $t\rightarrow\tau$? All such transformations are affine, in other words, proper time (atleast for null-like geodesics) are affine parameters which appear in the geodesic equations. But from the very definition of singularity, future null geodesics do not exists.