13


This is the logistic map:
. Image of bifurcation diagram of the logistic map
It is a fractal, as some might know here.
It has a Hausdorff fractal dimension of 0.538.
Is it possible to calculate/measure its fractal dimension using the box counting method?
A "hand waving calculation" is good enough.

Update: I understand there is another way to calculate the logistic map using the Kaplan-Yorke Conjecture. Can anyone explain that and how it can help calculating the fractal dimension of the logistic map?

Update2: Seems like the way to go around this is not Kaplan-Yorke Conjecture (which is a unproven Conjecture still), but use the correlation dimension. There is a paper with the solution here, hope I'll know more as I read it.

Abhimanyu Pallavi Sudhir
  • 6,268
GuySoft
  • 435

2 Answers2

6

Yes you can estimate the dimension by box counting. It is not quite hand waving but the idea has an advantage to be intuitive.

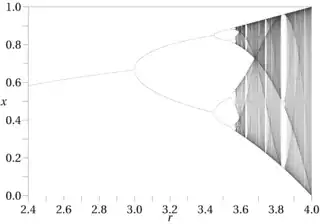
1) You consider the logistic map attractor like an analogy to a Cantor set whose dimension you can compute by box counting.

2) You remember that when the chaotic bands double, their sizes scale like $1/a$ and $1/a^2$ where $a$ is the second Feigenbaum constant, $a \approx 2.5029$. So the procedure looks like the Cantor set production because at each doubling you "remove" a part of the previous band. The difference being that the new smaller 2 parts have not the same size like in the Cantor set.

3) You suppose that at the Nth doubling you need $2^n$ boxes of size $R_n$ to cover the bands. Then at the $N+1$ stage you will need $2^{n+1}$ boxes of average size $$ R_{n+1} = \frac{R_n}{2}\left(\frac{1}{a} + \frac{1}{a²}\right). $$ The hand waving part is the arithmetical average because there is no rigorous reason to use it but one sees the idea of approximation.

4) The box counting dimension is then $$D_b = - \frac{\log 2}{\log(1/2(1/a + 1/a²))} = 0.544$$

You will admit that the hand waving was not so bad because one is not far from the much more rigorously derived value of $0.538$.

As a particular remark, the box counting is not very practical when the attractor is not strictly self similar like f.ex the Cantor set because the results depend then on the particularities of the covering method chosen

hbp
  • 174
Stan Won
  • 959
0

As the number of bifurcations goes to infinity, we can make some various claims.

$$d_f={{\ln(N)} \over {\ln(s)}}$$ Where $d_f$ is the fractal dimension, N is the number of boxes, and s is the scale.

(Examine $N\sim s^{d_f}$ to get the above)

$$N=2^n$$ And $$s \sim {\delta_f}^n$$ Where $\delta_f$ is the Feigenbaum constant.

We obtain, in the limit...

$$d_f \sim { {\ln(2)} \over {\ln(\delta_f)}}=0.4498...$$

Which has about 16% error from the empirical value of 0.538...

Zach466920
  • 1,137