What is the maximum spin of a particle? (Both theoretically and observed)

Question

I know that the elementary fermions are spin 1/2 and the elementary bosons are spin 1 (except the potential graviton), but are what is the highest known spin of any elementary particle (including their composites)?

Answer 1

A partial answer. Let's talk about hadrons. In experiment, how does one discover new hadrons? They examine the invariant mass of a certain combination of decay products and search for peaks in this distribution, employing angular distributions to measure the spin. In order to claim reliably a new state in a dataset of moderate size, one should ideally see a reasonably narrow mass peak, which is not overlapping with other states (i.e. no large interference effects).

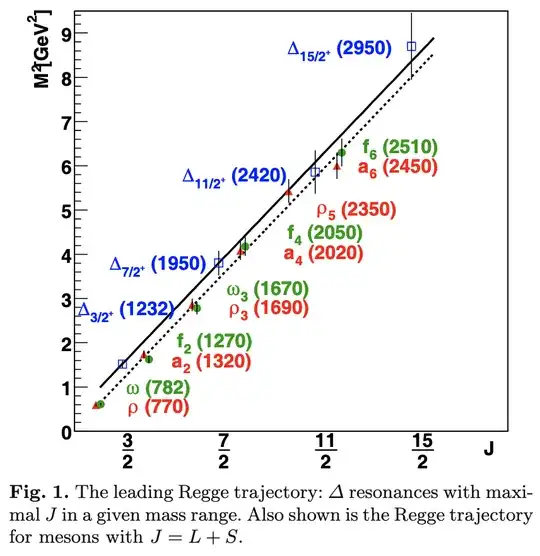
We know that for conventional hadrons (mesons and baryons, not talking about nuclei here), the higher its spin, the higher is its mass (figure taken from here):

The higher the mass, the more decay channels is available for a hadron. To a 0th order approximation, high-mass resonances are less stable, thus, broader than the low-mass resonances. (This is not always true due to conservation laws which might prohibit certain decays depending on quantum numbers of a given state). Also, the higher the mass, the lower is the cross-section to produce a given state in hadronic collisions or fixed-target experiments (once again, I am somewhat simplifying here).

Effectively, most states of a high spin have a high width, but low production cross-section, which makes the task of their separation from background rather difficult. And, philosophically, do we call something 'a hadron' if its lifetime is shorter than the characteristic timescale of a strong interaction?

For the hadrons made exclusively of the light quarks, there is a lot of data from hundreds of experiments, and states up to spin-6 (for mesons) such as $f_6(2510)$ and spin-15/2 (for baryons) such as $\Delta(2950)$, are established. There are some rumors about spin-7 mesons.

An important point is that in the quark model, it is often possible to interpret these states both as conventional meson/baryon states, or as exotic hadrons (tetraquarks, pentaquarks, glueballs etc).

Once we add heavier quarks, the experimental knowledge is less developed. For strange hadrons, the PDG tables know of a spin-5 $K^*_5(2380)$ meson and spin-9/2 $\Lambda(2350)$ baryon. For the charmonium, the recently discovered $\psi_3(3842)$ (spin 3) is the highest-spin known state, however, being exactly precise, its spin was not measured but rather 'guessed' from its properties.

Answer 2

A fully magnetised iron particle has spin $S \approx N_A \frac{5}{2} h$. Such large single Fe crystals can be are commercially available. Note that an Fe crystal can be seen as a composite of elementary particles.

Surely you were not after this answer though.