It is true that to maintain a constant acceleration that increases its speed relative to a rest frame, a rocket needs to spend increasing amounts of energy relative to that rest frame. Conservation of energy tells us this.
It is also true that a typical rocket (in space, assuming no outside forces) accelerates at a constant rate.
It is also true that a typical rocket uses chemical energy at a roughly constant rate.
But this seems impossible! The rocket accelerates at a constant rate, and to do this it must also increase the rate at which it uses energy, but it uses chemical energy at a constant rate. How can we reconcile these three facts?
The first piece of the puzzle is that the rocket will run out of fuel and reaction mass before it starts breaking conservation of energy. The rate it gains kinetic energy relative to the rest frame can never be greater than the rate it uses energy relative to the rest frame, and it must run out of fuel before that time.
The next piece of the puzzle is that when the rocket is going slowly, it is using its chemical energy very inefficiently. We know it must be, because the rate of kinetic energy increase is proportionally slower at low speeds, while the rocket's rate of use of chemical energy is the same. So, it has more power generation initially than it "needs" to increase its kinetic energy. The rocket is initially running well under its power capacity, and as it speeds up it starts to use the power more and more efficiently to increase its K.E., up until the point where it runs out of fuel.
Let's imagine a rocket that has a 100 kg payload and carries 900 kg of reaction mass. It begins stationary in space with no external forces acting on it. It constantly throws 1 kg/s of reaction mass backwards at 1000 m/s relative to itself. This means the reaction mass exerts a constant force of F = 1000 kg m / s^2, or 1000 N, on the rocket. It also means that the power exerted by the rocket, in the rocket's frame, is 1/2 * 1 kg/s * (1000 m/s)^2 = 500 kW.
The velocity of the rocket at time $T$ is $v(T) = \int_0^T a(t) dt = \int_0^T 1000 / m(t) dt = \int_0^T 1000 / (1000 - t) dt = 1000 (-\ln |1000 - T| + \ln |1000|)$
The velocity of exhaust (in the initial stationary frame), $v_e(T)$, is always $v(T) - 1000$ m/s.

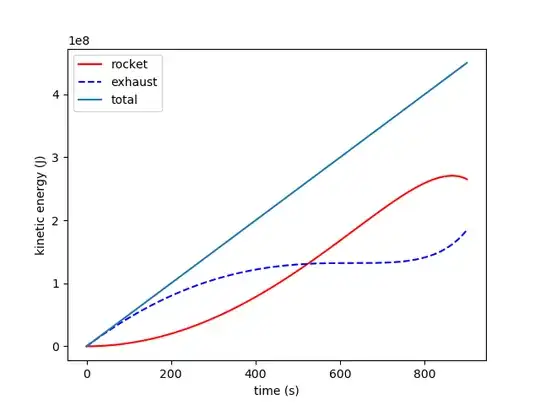
The energy of the rocket at time T is $1/2 m(T) v(T)^2$.
The total energy of the exhaust at time T is obtained by integrating over the energy of each piece of exhaust. It is $\int_0^T 1/2 v_e(t)^2 dt
= 1/2 \int_0^T (1000 (-\ln |1000 - t| + \ln |1000|) - 1000)^2 dt$.
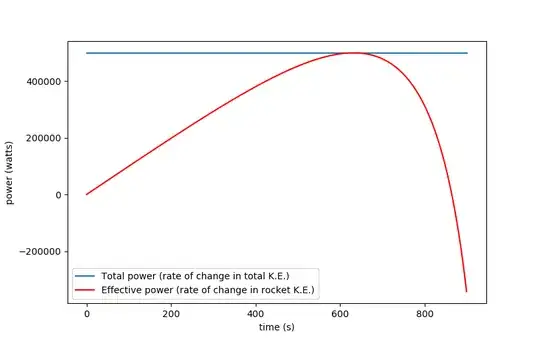
The total power output is obtained as the rate of increase of kinetic energy of rocket + exhaust. We already knew this should be 500 kW, and indeed it is.
The effective power output is the rate of increase of kinetic energy of the rocket. This is small at the beginning, as most of the kinetic energy is going into the exhaust, then increases to a maximum when the rocket is going 1000 m/s (because at this instant none of the energy is going into the exhaust, because the exhaust is stationary in the initial frame), and then decreases again as the rocket accelerates further. It actually goes negative at the end because the rocket is losing mass "more rapidly" than it is accelerating.