Yes, many constants could be changing and we wouldn't know...
It's possible that an expansion of all length scales can be happening, as in the cartoon below.
It shows all lengths increasing, the size of atoms, people, stars and the distances between all objects.
Each physical quantity and constant varies depending on the number of length dimensions in it. For example since Planck's constant has a length dimension of 2, so it's change with time is
$h=h_0e^{2Ht}$
where $H$ is an expansion constant and $t$ is time.
\begin{array}{c|c|c}
{quantity} & {length-dimension} & {change}\\
\hline
length & 1 & e^{Ht}\\
mass & 0 & constant\\
time & 0 & constant\\
h & 2 & e^{2Ht}\\
c & 1 & e^{Ht}\\
G & 3 & e^{3Ht}\\
Area & 2 & e^{2Ht}\\
\end{array}
etc...
It would be hard to rule out such an expansion and changing of constants, especially if the redshift of light from distant stars is regarded as due to it. If the energy of a photon is conserved during flight, but was emitted when Planck's constant was lower, then from $E=hf$, the frequency of the received photon would be lower and the light from a distant star would be redshifted.
It also leads to the conclusion that the matter density would be measured to be $0.25$ or $0.33$ from galaxy clusters and supernovae data respectively. A Diagram of supernovae data is below and then more details of the calculations.
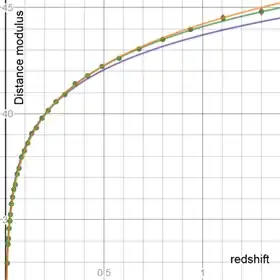 and
and 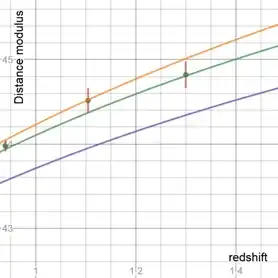
The diagrams show the distance modulus predicited by this type of expansion, top curve. Concordance cosmology with a matter density of 0.3 and 1.0 are the middle and bottom curve respectively. The second diagram is an enlargement of the first.
Matter density from Galaxy Clusters etc...
Traditionally the scale factor of the universe at redshift $z$ is
$a=\frac{1}{1+z}\tag{1}$
If the energy of the photon is conserved during flight, from $E=hf$ and $h=h_0e^{2Ht}$
For an emitted wavelength of $\lambda_1$
$z=\frac{\lambda_1e^{2Ht}-\lambda_1}{\lambda_1}$
$1+z = e^{2Ht}=a^{-2}$ ,
($a$ decreases with increasing $z$ in an expanding universe)
so
$a=\frac{1}{\sqrt{1+z}}\tag{2}$
For small distance $d$
$\frac{v}{c} =z= e^{2H\frac{d}{c}}-1=\frac{2Hd}{c}$
$v=2Hd\tag{3}$
i.e. Hubble’s law is still valid but we identify the expansion parameter $H$ with half of Hubble’s constant $H_0$
this leads to the conclusion that the matter density will be measured to be $\frac{1}{4}$ of the true value, as follows.
$\Omega_m = \frac{\rho}{\rho_{crit}}\tag{4}$
$\rho_{crit}=\frac{3H(z)^2}{8\pi G}\tag{5}$
If the value for $ H(z)$ used in $\rho_{crit}$ is twice the true value, then the apparent matter density would be measured as $0.25$ instead of $1$.
Matter Density from Supernovae Data.
In LCDM the Hubble parameter is
$H(z)=H_0\sqrt{\Omega_m {(1+z)}^3+\Omega_k{(1+z)}^2+\Omega_\Lambda}$
The comoving distance is obtained from
$D_M=\int_0^z \frac{c}{H(z)} dz$
Using a flat universe approximation, omitting $\frac{c}{H_0}$ and using $m$ for $\Omega_m$ ,the comoving distance, for small $z$ is
$\int_0^z(m(1+3z+3z^2+\dots )+1-m)^{-\frac{1}{2}}dz$
$=\int_0^z(1+3mz+3mz^2)^{-\frac{1}{2}}dz =\int_0^z(1-\frac{3}{2}mz+\dots)dz$
$=z-\frac{3mz^2}{4}\tag{6}$
For the type of expansion that we hope to rule out,
The co-moving distance is
$D_M=\int_t^0 \frac{c}{a(t)} dt$
$a=\frac{1}{\sqrt{1+z}}$
$\frac{da}{dt}=\frac{da}{dz} \times \frac{dz}{dt} ={-\frac{1}{2}(1+z)^{-\frac{3}{2}}}\times\frac{dz}{dt}$
$H(z)=H=\frac{\dot{a}}{a}=\frac{-1}{2(1+z)}\times\frac{dz}{dt}$
$dt=\frac{-1}{2H(1+z)}dz$
$D_M=\int_0^z \frac{c}{2H}{(1+z)}^{-\frac{1}{2}} dz$
$D_M=\frac{2c}{H_0}(\sqrt{1+z}-1)\tag{7}$
again omitting $\frac{c}{H_0}$ and for small $z$, $(7)$ becomes
$2(1+\frac{1}{2}z-\frac{1}{8}z^2-1)$
$=z-\frac{z^2}{4}\tag{8}$
there is a match between $(6)$ and $(8)$ if $m=\frac{1}{3}$
So we conclude from Galaxy and supernovae data, or combinations of data sets, that the matter density would be measured, with this type of expansion, at between $0.25$ and $0.33$. As it is measured at this value, it's concluded that the expansion cannot be ruled out this way. A diagram with supernovae data is above.
So the answer to your question is that the fundamental constants could be changing in proportion - and as such a changing constants situation actually matches all observations, it is very difficult to rule it out.


