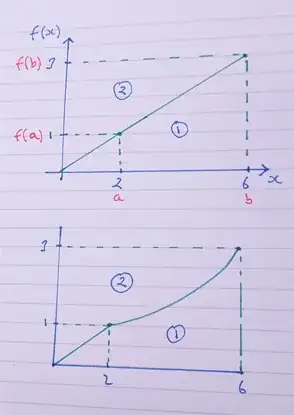
The definition of work done in moving the object from a to b using integral is $$W=\int_{a}^{b}f(x) \,dx$$ where the force F is a function of displacement x, namely $F=f(x)$
It is makes so much sense to me that the interval [a, b] is divided evenly into arbitrarily many subintervals $\Delta x$, and the work done during each subinterval is $f(x_{i}^{*})\Delta x$, where $x_{i}^{*}$ is the sample point. Then add these subintervals of work done together and take the limit, we have the work done formula $$W=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}{f(x_{i}^{*})\Delta x}=\int_{a}^{b}f(x) \,dx$$
If the displacement x is a(n) (inverse) function of F, that is, $f^{-1}(F)=x$, then it is also very plausible that the work done is $$W=\int_{f(a)}^{f(b)}f^{-1}(F) \,dF$$Because the force F is divided into arbitrarily many subintervals $\Delta F$, and the work done during each subinterval is $f^{-1}(F_{i}^{*})\Delta F$, where $F_{i}^{*}$ is sample point. By the similar idea and thought as above, I conclude that $$W=\lim_{n \rightarrow \infty}\sum_{i=1}^{n}f^{-1}(F_{i}^{*})\Delta F\int_{f(a)}^{f(b)}f^{-1}(F) \,dF$$
However, the second work done formula $W=\int_{f(a)}^{f(b)}f^{-1}(F) \,dF$ is wrong! In terms of Methematics, we can see from the F-x graph that $$W=\int_{a}^{b}f(x) \,dx=bf(b)-af(a)-\int_{f(a)}^{f(b)}f^{-1}(F) \,dF$$ This is the property of integral of any inverse function. But in terms of Physics, I think that I use the correct idea of integration to find work done. Because with respect to displacement x, the upper limit and the lower limit of the definite integral are a and b, respectively, which means that the object is at the point x=a in the beginning and at the point x=b in the end. With respect to to force F, the integral also makes sense to me, since the upper limit and the lower limit are f(a) and f(b), respectively, which represents that in the beginning, the force is F=f(a) and in the end, the force is F=f(b).
My question is: what's wrong with my second 'fantastic' idea work done formula $W=\int_{f(a)}^{f(b)}f^{-1}(F) \,dF$? Why could we only divide the displacement x into arbitrarily many subintervals instead of dividing the force F? Can anyone help me out? Thank you so much!