1

To get it straight, Charge symmetry can be broken by U-236 atoms, Parity can be broken by K-one atoms and Time symmetry can be broken by quarks. So, how do they together hold true?

dotmashrc
  • 364

1 Answers1

1

As a basic analogy consider the following shape in 3D. 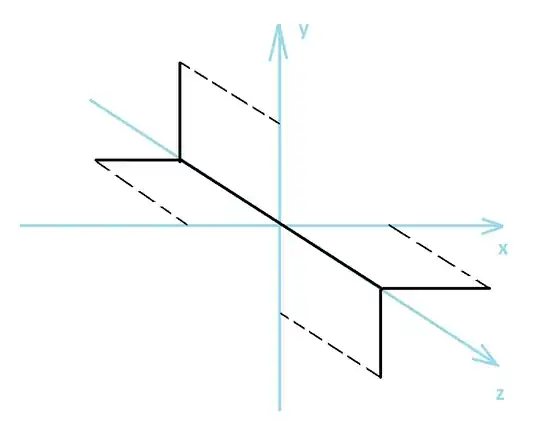Inverse-symmetric shape It is not symmetric under reflections of the $x$ axis. Neither it is symmetric under reflections of the $y$ axis or the $z$ axis. It is also not symmetric under any combinations of two of these reflections, say if you first reflect the $x$ axis and then reflect the $y$ axis. However if you reflect all three axis the shape transforms into itself.

The interaction that violates most discrete symmetries in the Standard model is the $W^{\pm}$ interaction (which is part of the weak interaction). The corresponding term in the Lagrangian looks like this (I write for quarks, for the leptons it looks similar), \begin{equation} \int d^4x\Big((u_{iL})^\dagger V_{ij} W_\mu^{+}\bar{\sigma}^\mu d_{jL}+\mathrm{h.c.}\Big) \end{equation} Under the spatial reflection ($\mathcal{P}$) the left-handed and right-handed components of the spinors are interchanged \begin{equation} \mathcal{P}: \psi_L(t,\vec{x})\mapsto \psi_R(t,-\vec{x}), \quad \psi_R(t,\vec{x})\mapsto \psi_L(t,-\vec{x}) \end{equation} \begin{equation} \mathcal{P}: W_0^{+}(t,\vec{x})\mapsto W_0^{+}(t,-\vec{x}), \quad W_k^{+}(t,\vec{x})\mapsto -W_k^{+}(t,-\vec{x}),\,k=1,2,3 \end{equation} Similarly the charge conjugation ($\mathcal{C}$) not only conjugates the fields but also exchanges the left and right components of the spinors, \begin{equation} \mathcal{P}: \psi_L(t,\vec{x})\mapsto -i\sigma_2\psi_R(t,\vec{x})^\dagger, \quad \psi_R(t,\vec{x})\mapsto i\sigma_2\psi_L(t,\vec{x})^\dagger \end{equation} \begin{equation} \mathcal{P}: W_0^{+}(t,\vec{x})\mapsto -W_0^{-}(t,\vec{x}), \quad W_k^{+}(t,\vec{x})\mapsto -W_k^{-}(t,\vec{x}),\,k=1,2,3 \end{equation}

Because only the left components participate in the weak interaction, we immediately see that $\mathcal{P}$ and $\mathcal{C}$ are both violated - they both transform the interaction term into the one containing only the right components of the spinor fields i.e. of the form $u_R^\dagger W_\mu\sigma^\mu d_R$. However the combination of these two transformations transforms the left-handed spinors to the left-handed spinors. So you may suspect that the combined transformation $\mathcal{CP}$ would leave this interaction term invariant. This happens to be true for the similar interaction with $Z$-bosons - it violates $\mathcal{C}$ and $\mathcal{P}$ separately but is invariant under the combination $\mathcal{CP}$. However the interaction with $W$ bosons contains the Cabbibo-Kobayashi-Maskawa (CKM) matrix $V_{ij}$. Under the combined $\mathcal{CP}$ transformation this interaction term transforms not into itself but into the one with complex conjugated CKM-matrix, \begin{equation} V_{ij}\mapsto V_{ij}^\star \end{equation} So if $V$ is complex (which it is) this term violates the combined $\mathcal{CP}$ symmetry. However the time reversal transformation is antilinear - i.e. it involves the complex conjugation of all parameters and the resulting transformation of the interaction term is again the complex conjugation of the CKM-matrix. So separately $\mathcal{CP}$ and $\mathcal{T}$ change this interaction term but their combination $\mathcal{CPT}$ leaves it invariant.

OON
  • 9,214