How can we determine the electric charges of quarks? And what are the values? The color charge is not the electric charge...
How do we even know their electric charge? I would think that there are more ways how the quarks' charge could be distributed.
It starts out as a model parameter. With
$$ p\rightarrow |uud\rangle$$ $$ n\rightarrow |udd\rangle$$
the charges satisfy:
$$ 2q_u + q_d = q_p = 1 $$ $$ q_u + 2q_d = q_n = 0 $$
(in terms of $+|e|$), which is solved by $q_u=+\frac 2 3$ and $q_d=-\frac 1 3$. Interactions with pions and other hadrons do not contradict this.
The only way to measure the quark charge is by probing the nucleon with something that "sees" charge; e.g., photons. A beam of electrons provided a source of virtual photons, and can be scattered of nucleons:
The wavelength ($\lambda$) of the virtual photon is related to experimental observables via the momentum transfer ($Q^2$):
$$\big(\frac{\hbar}{\lambda}\big)^2 = Q^2\approx 4EE'\sin^2(\frac{\theta}2)$$
and the energy is:
$$ \nu = E-E'$$
With both the electron and quark being fundamental spin 1/2 point particles, their scattering interaction is defined by the Mott cross-section. Scattering from the spin-1/2 proton is then parameterized by two structure functions:
$$\frac{d\sigma}{d\Omega dE}=\frac{4\alpha^2E^2\cos^2{\frac{\theta}2}}{Q^2}\Big[ W_2(\nu, Q^2)+W_1(\nu,Q^2)\tan^2{\frac{\theta}2} \Big] $$
Mixtures of the two $W_i(\nu, Q^2)$ describe scattering from electric and magnetic terms.
As $Q^2\gg M_P^2$, the scattering is parameterized with different (but ultimately equivalent) structure functions $F_1$ and $F_2$:
$$\frac{d\sigma}{dx dy}=\frac{4\alpha^2ME}{Q^2}\Big[ \frac{y^2}2 2xF_1(x, Q^2)+(1-y)F_2(x,Q^2) \Big] $$
where the Bjorken $x$ and $y$ are as follows.
$$ x = \frac{Q^2}{2M_p\nu} $$
is the momentum fraction, or the fraction of proton momentum carried by the struck quark. Note the $0\lt x\le 1$, where $x=1$ is elastic scattering. The fact that there is a peak at $x=\frac 1 3$ shows the proton behaves has a bag of 3 non-interacting quarks.
$$ y = \frac 1 2 (1-\cos{\theta}) $$
is the fractional energy loss of the incoming particle. Note that $0\lt y \le 1$, and that both $x$ and $y$ are Lorentz invariant.
$y=\frac 1 2(1-\cos{\theta})$
At high $Q^2$, the scattering from the proton (or neutron) is an incoherent sum over Mott-scattering from valence and sea quarks inside the proton. The proton's structure can then be described by structure functions that parameterize the quarks in the nucleon.
Because quarks have no structure, and are spin 1/2, the scattering is indented of $Q^2$ (there is no inherent length scale), and the Callan-Gross relation:
$$ 2xF_1(x) = F_2(x) =\sum_i q^2_ixf_i(x) $$
holds. The sum is over (anti)quark flavors. The $f_i(x)$ are the momentum fraction of quarks of flavor $i$; they are called quark structure functions, and are sometimes written explicitly as:
$$ f^p_u(x) = u(x) = f^n_d(x)$$ $$ f^n_d(x) = d(x) = f^p_u(x)$$
where the superscript refers to a proton or neutron target. (They are isospin symmetric). Note also that the charge has explicitly entered the chat.
With that and both proton and neutron targets:
$$F_2^{eP}(x) = \frac 4 9 x(u(x)+\bar u(x))+\frac 1 9 x(d(x)+\bar d(x))$$
$$F_2^{eN}(x) = \frac 1 9 x(u(x)+\bar u(x))+\frac 4 9 x(d(x)+\bar d(x))$$
Additional model dependent assumptions are that the antiquark distributions satisfy:
$$\bar u(x)=\bar d(x)=\bar s(x)\equiv S(x) =u_{sea}(x)=d_{sea}(x)=s_{sea}(x) $$
and that the quarks distributions can be separated into valence and sea terms:
$$u(x) = u_{val}(x)+u_sea(x)=u_{val}(x)+S(x)$$ $$d(x) = d_{val}(x)+d_sea(x)=d_{val}(x)+S(x)$$
Data show:
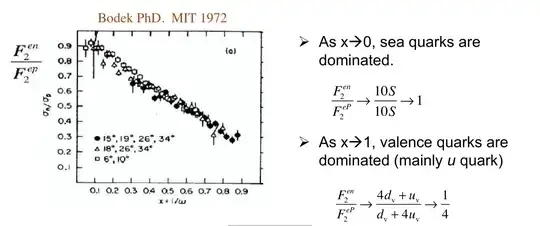
which validates $|q_u/q_d|= 2$. The absolute magnitude:
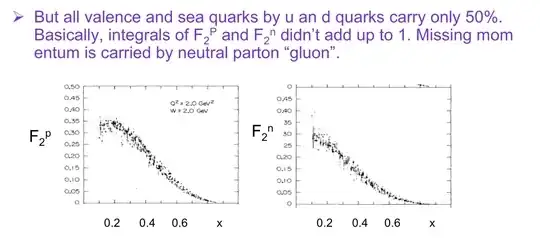
cannot be used to get an absolute measurement of the charge. Half the signal is missing because neutral gluons carry half of the proton momentum.
Other charge dependent relations that are measured in deep inelastic scattering are:
The Gross-Llewellyn Smith Sum Rule:
$$ \int_0^1(u_v(x)+d_v(x))dx=3 $$
The Gottfried Sum Rule:
$$\int_0^1(u_v(x)-d_v(x))dx=1$$
Measurement of these verify the charges in the quark model.
