0

I was thinking about a really simple inverted pendulum of length $L$, mass $M$ and made this free-body diagram:

1

I decided to apply Newton's second law relative to the origin (pivot) and to the centroid (location of the force $F_g$), giving equations (1) and (2) respectively:

$$\sum \tau_{o}=-F_{g}\cdot \frac{L}{2}\sin\left( \theta \right)=I_0 \ddot{\theta} \tag{1}$$ $$\sum \tau_{c}=H\cdot \frac{L}{2}\cos\left (\theta\right)-V\cdot \frac{L}{2}\sin\left(\theta \right)=I_{c}\ddot{\theta} \tag{2}$$

If I consider the pendulum as a rod, $I_c=ML^2/12$ and $I_0=ML^2/3$. Are both approaches valid? Do they give the same response of the system?

Vincent Thacker
  • 15,416
Enzo Charles
  • 3

1 Answers1

0

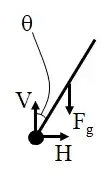
No, the two approaches, as you have presented them, would not be equivalent. The first one is accurate. The second is not. You are missing the Newton's equations for the motion of the center of mass of the rod. With their help you would be able to express the components $H$ and $V$ of the reaction force and plug them in the torque equation to reach an equation, equivalent to the one from the first approach.

\begin{align} & x_c \,\hat{i} \, + \, y_c\,\hat{j} \, = \, \frac{L}{2}\,\sin(\theta) \, \hat{i} \, +\, \frac{L}{2}\,\cos(\theta) \, \hat{j} \end{align}

The full set of equations of motion are

\begin{align} & M\frac{d^2}{dt^2} \big(\, x_c \,\hat{i} \, + \, y_c\,\hat{j} \,\big) \,=\, H \, \hat{i} \, + \,V \, \hat{j} \,- \,Mg\,\hat{j}\\ &\\ &I_c\frac{d^2\theta}{dt^2} \,\hat{k} \, = \, \big(\, - x_c \,\hat{i} \, - \, y_c\,\hat{j} \,\big)\times \big(\,H \, \hat{i} \, + \,V \, \hat{j}\,\big) \end{align}

Plug expressions

\begin{align} & \frac{ML}{2}\,\frac{d^2}{dt^2} \big(\, \sin(\theta) \, \hat{i} \, +\,\cos(\theta) \, \hat{j} \,\big) \,=\, H \, \hat{i} \, + \,\big(\,V \,- \,Mg\,\big)\hat{j}\\ &\\ &I_c\frac{d^2\theta}{dt^2} \,\hat{k} \, = \, -\,\frac{L}{2}\big(\, \sin(\theta) \, \hat{i} \, +\,\cos(\theta) \, \hat{j} \,\big)\times \big(\,H \, \hat{i} \, + \,V \, \hat{j}\,\big) \end{align}

Perform most of the operations \begin{align} \frac{ML}{2}\, &\Big[\,-\sin(\theta)\frac{d^2\theta}{dt^2} - \cos(\theta)\Big(\frac{d\theta}{dt}\Big)^2\,\Big] \hat{i} \, \\ +\, \frac{ML}{2}\,&\Big[\,\,\,\,\,\,\,\cos(\theta)\frac{d^2\theta}{dt^2} - \sin(\theta)\Big(\frac{d\theta}{dt}\Big)^2\,\Big] \, \hat{j} \,=\, H \, \hat{i} \, + \,\big(\,V \,- \,Mg\,\big)\hat{j}\\ &\\ &I_c\frac{d^2\theta}{dt^2} \,\hat{k} \, = \, \frac{L}{2}\big(\, H\cos(\theta) - V\sin(\theta) \,\big) \hat{k} \end{align}

Solve for the horizontal and vertical components of the reaction force \begin{align} &H \, =\, \frac{ML}{2}\, \Big[\,-\sin(\theta)\frac{d^2\theta}{dt^2} - \cos(\theta)\Big(\frac{d\theta}{dt}\Big)^2\,\Big] \\ &V \, = \, \frac{ML}{2}\,\Big[\,\,\,\,\,\,\,\cos(\theta)\frac{d^2\theta}{dt^2} - \sin(\theta)\Big(\frac{d\theta}{dt}\Big)^2\,\Big] \, +\, Mg\\ &\\ &I_c\frac{d^2\theta}{dt^2} \, = \, \frac{L}{2}\, H\cos(\theta) - \frac{L}{2}\, V\sin(\theta) \end{align}

and plug them in the third (torque) equation, simplify and apply the appropriate trigonometric identities. The result is

$$ I_c\frac{d^2\theta}{dt^2} \, = \, -\,\frac{ML^2}{4}\,\frac{d^2\theta}{dt^2} \, -\, \frac{MgL}{2} \sin(\theta) $$

or re-expressed $$ \left(I_c\, + \,\frac{ML^2}{4}\right)\frac{d^2\theta}{dt^2} \, = \, -\, \frac{MgL}{2} \sin(\theta) $$

where $$I_o \, =\, I_c\, + \,\frac{ML^2}{4}$$ which is in line with the parallel axis theorem.

Futurologist
  • 2,621