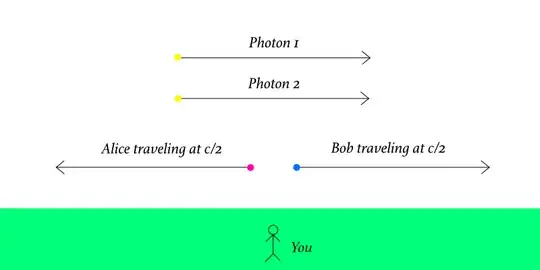
Speed of light is absolute, unlike other speeds which are relative to each other, right? Below is an image of a scenario that illustrates my question. If Alice is moving at $c/2$ in one direction and Bob is moving at $c/2$ in the opposite direction, then from Alice point of view Bob would be moving at the speed of light, no? So Photon 1 and Bob would be moving at the same speed according to Alice. Since they are also moving in the same direction, after some time $t$ has passed they should have traveled the same distance $d$ away from her. So is Bob moving at the speed of light? But then again, the speed of light is absolute and Bob should also be moving at the speed of light from our perspective (standing on the ground watching all of this), no?
On the other hand to Bob Photon 1 is still moving at $c$, so they are not moving at the same speed according to Bob. So after time $t$ Photon 1 will have traveled distance $d$ away from Bob. But isn't this a contradiction?
It might well be that a very similar question has been asked before, but since I do not know the answer I do not know what to look for.