In many artistic impressions or movies there are pictures or scenes where the sky is filled with an enormous moon (as seen from a planet) or vice versa. I wonder if there is an upper limit to the apparent size when viewed with the naked eye (no tele lens). Since the Roche Limit forbids celestial bodies coming too close to each other, there certainly is a limit to the apparent size.
The Roche limit applies when the astronomical body in question is held together by gravity rather than electromagnetic forces. This is the case for bodies with a diameter larger than around 500km. Obviously for smaller bodies, like humans, we can get arbitrarily close to the surface, but i suspect this isn't what you're asking about.
For moons much smaller than the planet they are orbiting, and assuming the moon and the planet have roughly equal densities, the Roche limit is about 2.44$R_P$, where $R_P$ is the radius of the planet.
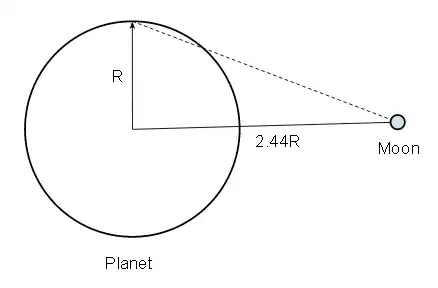
The angle subtended by the planet from the Moon is 2 arctan(1/2.44) or about 45º. So assuming you take the sky to cover 180º, at the Roche limit the planet will cover a quarter of the sky (by width, rather less by area!).
If the density of the moon is much greater than the planet the Roche limit will be reduced and the planet can look bigger, and likewise if the density of the moon is lower the maximum size of the planet would smaller. However the Roche limit varies as the cube root of the density ratio, so you need a big density difference to make much difference to the Roche limit.
Response to comment:
If you include the densities the expression of the Roche limit is:
$$ d = 2.44 R_P \left( \frac{\rho_P}{\rho_M} \right)^{1/3} $$
where $\rho_P$ is the density of the planet and $\rho_M$ is the density of the moon. The average density of Jupiter is 1.33kg/m$^3$ and the average density of the Moon is 3.35kg/m$^3$, and substititing these values gives the Roche limit as 1.79$R_P$. Using the formula for the angle gives about 58º.
You can use the formula to calculate what density ratio is required for the Roche limit to fall to $R_P$, i.e. for the moon to touch the planet's surface. The required density ratio is about 15. This could be attained for Jupiter if the moon was made of pure osmium (the densest element) but this is, to say the least, unlikel;y to occur in nature.
In addition to the astronomical explanations above, there is theoretical way to create a view like the one pictured above (!) for any actual size of planet and satellite.
Consider the closing shot from Indiana Jones and the Holy Grail, where the victorious archaeologists are riding off into the huge setting sun. The sun subtends about 0.5 degrees as viewed from the earth, so we first select a lens for the camera with a focal length that gives the camera a field of view the same size, 0.5 degrees. The sun will fill the field of view.
Now, a person on horseback is about 2.5 metres tall. If we position the rider$\frac{2.5}{\sin(0.5)}=286$ metres away from the camera, then the rider will also appear 0.5 degrees high. Make sure that the rider is on a line between the camera and the setting sun, and you're all set...
