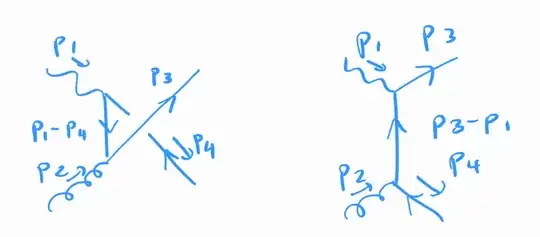Photon-Gluon annihilation in QCD

Question

I am starting to learn about QCD, and I wanted to calculate the squared matrix elements for photon-gluon annihilation into a quark and an anti-quark. However, I am having trouble writing down the correct matrix elements at tree level and computing the spin and color sum of the averaged matrix element.

I found this FeynCalc webpage, but I did not find it extremely helpful. I would really appreciate any help or resources.

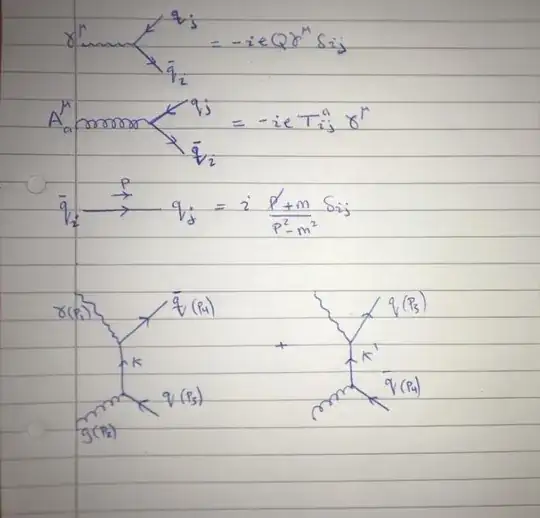
The specific process I am interested in is $$\gamma(p_1)+g(p_{2})\rightarrow q(p_{3})+\bar{q}(p_{4}).$$ So the relevant Feynman rules and diagrams are:

I believe that I have made a mistake with the arrows on the first (left) diagram; I think they should be in the opposite direction. Thus the matrix elements for the first (left) diagram and the second (right) diagram are: $$M_{1} = -ie^2Q\left(v(p_{4})T^b \gamma ^{\alpha}\left(\frac{\not{p_{1}}-\not{p_{4}}+m}{(p_{4}-p_{1})^2-m^2}\right)\gamma^{\beta}\bar{u}(p_{3})\epsilon_{\alpha}(p_{1})\epsilon_{\beta}(p_{2})\right)$$ and $$M_{2} = -ie^2Q\left(\bar{u}(p_{3}) \gamma ^{\mu}\left(\frac{\not{p_{3}}-\not{p_{1}}+m}{(p_{3}-p_{1})^2-m^2}\right)T^a\gamma^{\nu}v(p_{4})\epsilon_{\mu}(p_{1})\epsilon_{\nu}(p_{2})\right)$$ However, I am still not sure that I have applied the rules correctly.

Answer 1

There are some errors.

The fermion line on the left diagram should be reversed, since the fermion is outgoing. Then one should trace the fermion line backwards, so you have $$ \bar{u}(p_3) ... v(p_4) $$ on both diagrams. I assume you know that the spinors are vectors in the Dirac space in which the gamma matrices live, so this expression is a scalar in this space, $\bar{u}$ is a row vector and $v$ is a column vector.

Then one usually draws another reverse arrow over the outgoing fermion line to imply that it is actually outgoing.

I drew it for you. This are all the diagrams that contribute on tree level.

Then you should of course note that photon and gluon couplings are not equal! So you better use different symbol for them, conventionally $e$ for em coupling and $g$ for the strong coupling.