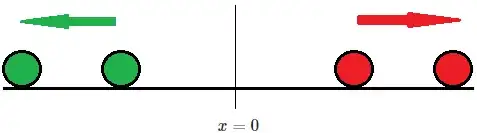Not a demonstration, but maybe something more visual than the other correct answers.
Instead of being in 2D like you suggest, let's try to see what happens in 1D when the particles move "radially" outward of $x=0$. Green balls go to the left at a constant momentum $-p$ and red balls go to the right at the same absolute momentum $p$ (I suppose they all have the same absolute velocity. The argument is way easier to explain this way... Even though you are asking for different momenta...)
In the phase space, this configuration gives at two different times:
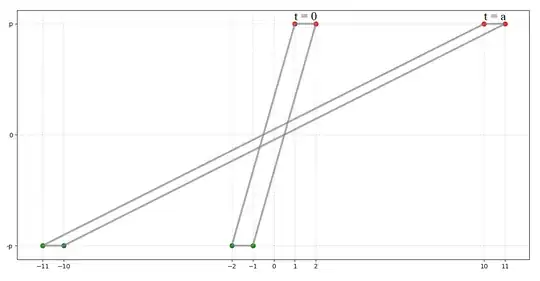
The momentum doesn't change since there is no force (so same $y$ value whatever $t$ is) and the distance between two balls of the same color (in the real space) will be the same at any time (the distance between my 2 green balls et my 2 red balls is $1$ in my awful figure).
I also tried to draw the surface area (ie volume in $d>2$) in gray at time $t=0$ and at a later time $t=a$.
Now, the area of these parallelograms (the "volume" bounded by our 4 balls at $t=0$ or $t=a$) is of course the height of the parallelogram times the lenght of its base. It's trivial to see that on the figure, both parallelogram have then the same area. So the volume bounded by the 4 balls is constant although in real space, the balls move in opposite directions.
edit
It also works in the case of different momenta (even though, it's kind of harder to see (I changed the position of 2 balls so that the calculation of the area is easier)). We could have taken a different absolute momentum for each particle, but we would lose the symetry and thus, it would be hard to calculate the area (for example, taking one momentum equal to 0 like you suggest would make the conservation of the area hard to see visualy).
I'm not sure I understand your comments but I'll try to answer.
Yes, I plotted points but we're not talking about the volume of these points, we are talking about the volume bounded by a cloud of points (so 3 points are required).
We can also view this area as a density of probability, so even if in classical mechanics a particle is Dirac delta (it takes no volume) in the phase space, it's not really what the Liouville theorem is dealing with (at first at least). For example, we can say that we don't really know where our particle (with 0 volume) is, but we are sure that it's located in a tiny square (or parallelogram) of area $A$ in phase space with an uniform probability. Then, what we can say is, after some time, the particle will still be located inside a surface of area $A$ (but not necessarily a square).
This explanation is not very general, but kind of useful.
Now, we talk about conservation of volume because $dpdx$ at time $t$ is equal to $dxdp$ at time $t'>t$. This is equivalent to the assertion I mentioned above, namely: the probability distribution is constant along (so following the fluid) a classical trajectory in phase space. Where $dx$ and $dp$ are the horizontal and vertical lenghts of your fluid element (or your cloud of points, since these are the same).
At the end of the day, all you want is to define a volume, be it a probability density with your fluid elements mentionned in your comments, or an area bounded by points like in my figures, and show that this volume in conserved. The probability density/fluid approach is better understood using $\frac{d\rho}{dt}=0$ (see the wiki page), while the volume approach is better understood by seeing that $dx(t)dp(t)=dx(t+dt)dp(t+dt)$ because of the egality of the mixed derivative of the Hamiltonian. But they are both equivalent.
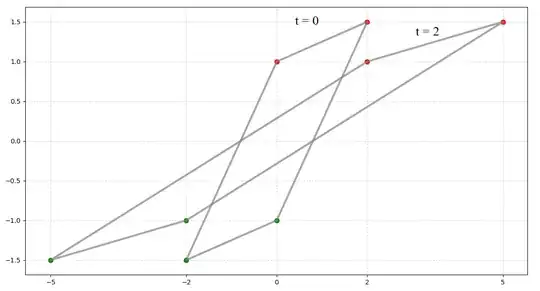
Still talking about your second comment, here is the "fluid approach" (my first figures take the "volume bounded by every points" approach, but I repeat both are equivalent) 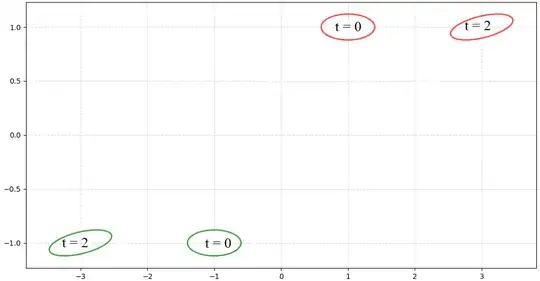
So now, as you proposed, we take 2 fluids elements instead of 1 to describe 4 particles (it could be troublesome to do so but, let's assume nothing too serious happens at $t>0$).
What is important here, is that, at $t = 0$ you don't consider that you perfectly know the position of your particles, you say: well, i've got 2 particles inside the top ellipse and 2 inside the bottom ellipse, but I don't know where (you define a probability density $\rho$). Then, you proceed to move every points inside these volumes according to their corresponding equations of motion. This gives a new volume/area (on the figure these are the outermost ellipses at $t=2$), these new clouds of points/clouds of particles/densities of probability/fluid elements (containing 2 particles each) have the same area that what we started with. Note that in this case, we do not care about the volume between the fluid elements!
I feel like I went all over the place, so it might no be very understandable but I wanted to give a lot of examples.