1

Refering to this closed question, I made a test using a fan, a styrofoam sheet and a scale as shown in the fig (a) and (b) 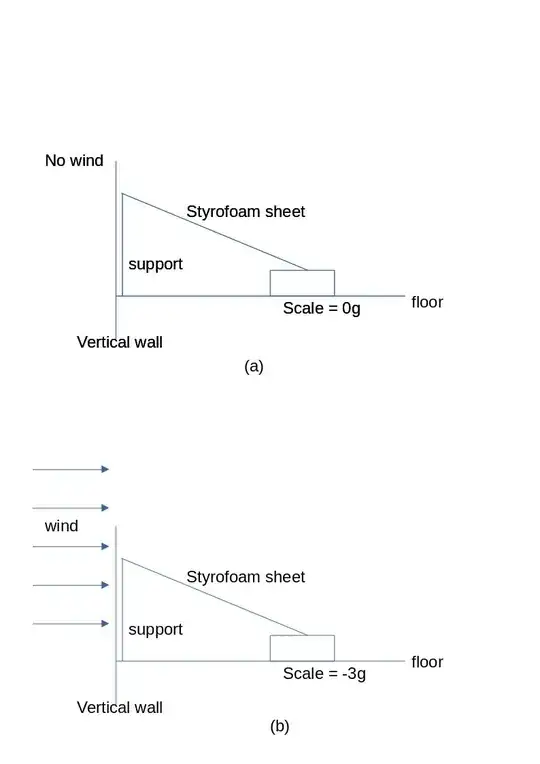below

Part of the weight of the sheet is supported by a rod close to the wall, and part by the scale. The scale shows 35 g if it is turned on before placing the load there. In order to better visualize the effect, I turned it on after the arrangement was done, without wind. In that way it shows 0g.

When the fan is turned on, the scale displays negative numbers, indicating the presence of a lift force. The force increases for increased fan velocity. The wind can only go to the right above the wall.

The intuitive explanation is that the wind creates a low pressure region above the sheet. My question is how the kinetic theory explains that "suction" effect? After all if the molecules are modeled as bouncing balls, with constant momentum between collisions, the average vertical component of the momentum should not be affected by the increased average horizontal momentum (the wind).

One additional question is: how to estimate that force as a function of the wind velocity?

Claudio Saspinski
  • 17,607

1 Answers1

0

Bernoulli's principle is easily stated by often difficult to actually explain. For your example, the idea is that as the horizontal air flow of a fluid increases the pressure exerted vertically decreases. This means as the air moves across the top of your Styrofoam sheet the pressure exerted downward is less than the pressure exerted upward by the air under the Styrofoam sheet. However, you have already come to this conclusion, but your question is why this occurs when the horizontal motion should have no impact on the vertical motion of molecules moving about.

It is true that each individual molecule applies the same downward pressure whether the air is moving horizontally or not. But, you must also consider the frequency with which the air molecules have an opportunity to impact the Styrofoam sheet as they pass across it. In general, the density of the air does not change so that you have the same density of molecules above the sheet as below. But when the air is moving horizontally each molecule has fewer opportunities to strike the surface within a given period of time. Yes, it is true that the horizontal motion has no effect on each individual molecules vertical motion (and therefore the force exerted). But what you have not considered is that the frequency of interactions per molecule decreases as the horizontal velocity increases.

Think of it this way. If you are standing in front of a punching bag you can punch it all day long. Now, if you are moving horizontally while throwing punches with the same force how many times will you hit the bag as you go by.

In summary, yes - each molecule of air strikes with the same vertical force, but the frequency of interactions between molecules of air and the Styrofoam sheet will decrease with increased horizontal velocity. This is what creates the pressure differential.

JRL
  • 788