Work done by Static friction

Question

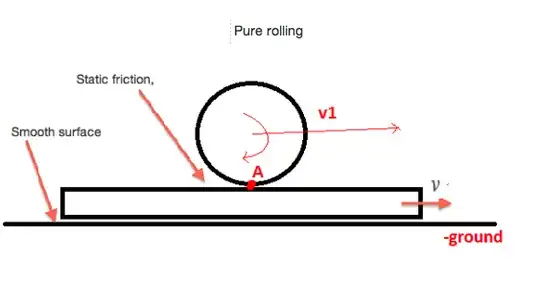
Here $v1$ is relative to the block on which sphere is pure rolling but static friction isn't $0$ as of now .

In the following diagram, is work done by static friction $0$ ?, since the point of application is also moving with speed $v$ w.r.t. ground here and is only stationary w.r.t. the block on which sphere is rolling w.r.t. ground here .

If it isn't $0$ , where is static friction increasing net Kinetic Energy of the rolling sphere?

The mass of the block which is on smooth surface $\rightarrow \infty$.

Additional comment : Because when we consider rolling w.r.t. ground of a new sphere, the net kinetic energy doesn't change . Rolling KE changes to translation KE or vice-vera depending upon situation . And now static friction should also do this in this case also , however , the deinition of work is also $\vec {F}\cdot \vec {dx}$ for point of application and and now point of application is always moving with $v$ w.r.t. ground, so according to this definition work is not $0$ . So is Kinetic Energy increasing somewhere w.r.t. ground? And if it isn't increasing there's something wrong with the way I am defining work ?

EDIT: You can also consider evaluating work for an incline plane wedge falling in free space which has a sphere rolling on it and gravity and air resistive forces are acting on both the rolling sphere and the inclined plane .

The inclined plane has attained terminal velocity and the rolling sphere is still accelerating along the incline only in net . and the inclined plane wedge's terminal velocity's direction is ** along the same direction with the horizontal as is the direction of the incline plane's slopy surface. ** And also mass of the incline plane wedge $\rightarrow \infty$.

Answer 1

In the following diagram, is work done by static friction 0 ?, since the point of application is also moving with speed v w.r.t. ground here and is only stationary w.r.t. the block on which sphere is rolling w.r.t. ground here.

Static friction itself is 0. The formula $f_s=\mu N$ defines the maximum possible magnitude of the static friction force, not the true static friction force. In this case, there is no other acceleration, so there is no need for static friction. Static friction only comes into play when the two bodies are attempting to be in relative motion with each other. This is not the case here, at the point of contact the velocities of the corresponding points on the wheel and platform are equal and there is no force trying to stop this.

When you're standing on the ground, you're not mysteriously being pushed by friction. It's the same thing here, the wheel is "standing" with respect to the point of contact, though the points of contact are changing over time.