Why do some particles speed up more than other particles (of the same plane) in a tube of decreasing cross section?

Question

This question is quite long (and stupid) and needs focus and patience while reading since there are seriously a lot of ideal assumptions. So please tolerate if possible.

---

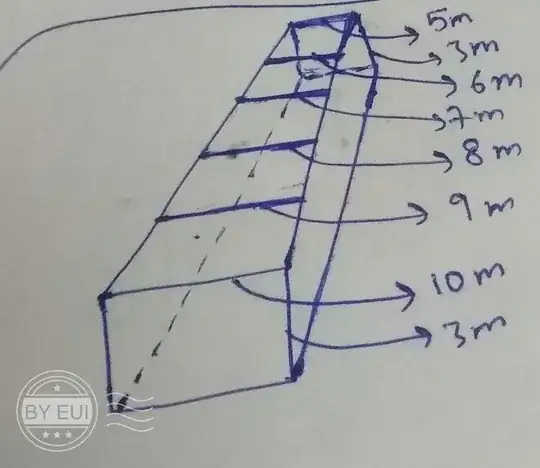
So suppose we a have a tube of rectangular cross section (as shown in the fig.).

Now let's assume that at t=0 we have a plane of molecules just entering the tube from the side with wider hole such that the speed of all the molecules in this plane is same (let's assume if not possible).

Here comes another assumption :

suppose the molecules in the entering plane are arranged in such an ordered manner and that the theoretical minimum possible distance between two adjacent molecules is $1 m$ (with respect to the units in the fig) and in this plane there are overall 30 molecules (this means that the molecules can't be further compressed) .

Now as they move forward and reach the second cross section (of area $27$$m^2$) the number of molecules in the plane must go down to 27. This means that out of 30 molecules only 27 could have the same speed variation as they moved from first cross section to the second one. Similarly if we continue this argument this will mean that after reaching the third cross section there will be only $24$ molecule sin the plane and so on.

This means that as we move ahead in the tube the number of molecules in the plane goes on decreasing. One can ask where are the other $3$ molecules going after each cross section is being crossed?*

So I would say it directly that "the $3$ molecules leaving the plane each time are having a greater change in speed than the majority of the molecules in their plane" .

I am making this claim on the basis of the fact that (number of molecules entering the tube must be equal to the number of molecules leaving it). So for $30$ molecules to leave , we must have $15$ such speeded molecules too so that they can join the other $15$ molecules in the plane of the last cross section.

But this comes down to another question (about which I don't know the answer) : What makes those $3$ molecules so special ? Why did they experience greater change in speed than the majority in their plane and how did this happen ?

Answer 1

What makes those 3 molecules so special ? Why did they experience greater change in speed than the majority in their plane and how did this happen ?

If we assume, for example, that collisions of molecules with the walls of the tube are elastic, the 3 molecules experience a greater change in velocity, not in speed (their speed remains the same, but the direction of motion changes). So these 3 molecules are different because they hit the walls of the tube within the first part of the tube, whereas the other molecules don't.

EDIT (6/26/2021). The question does not describe how exactly the molecules are ordered and how they collide with each other. Let me also note that if "the theoretical minimum possible distance between two adjacent molecules is 1 m (with respect to the units in the fig) and in this plane there are overall 30 molecules", that does not necessarily mean that " the molecules can't be further compressed", because there is no reason why the molecules cannot approach closely to the walls of the tube. Anyway, one can just run a computer model of the problem assuming some initial positions of the molecules and assuming that molecules collide with each other elastically (as 1 m diameter billiard balls with all their masses in their centers) and that they collide elastically with the walls of the tube as point particles. (If the molecules are not supposed to come closer than 1 m to the walls, then one just cannot find any allowable initial positions of the molecules.) As for the result of the modeling, I cannot predict it.

EDIT (6/26/2021): The OP explained that the molecules can come arbitrarily close to the walls of the tube. Then the problem is equivalent to a problem with 30 1-m diameter balls and a tube with walls displaced by 0.5 m with respect to the walls of the original tube. So one can model this problem, and it seems plausible that some balls will exit through the larger cross-section of the tube.

Answer 2

If the number of molecules is low enough, then the same number will fit through each part of your diagram, and the 'gas' will become denser as it flows down the tube.

If the number of molecules is high, and the substance is a liquid, then the density can't increase. Then it's true that the number that can fit in each section of the tube is reduced and the speed of the molecules is increased. That occurs due to collisions between the molecules.

Some molecules (like the three you mentioned), are held back due to the collisions, but the same collisions impart momentum to the other molecules that go through the next section, speeding those ones up.

Answer 3

let's assume that at t=0 we have a plane of molecules just entering the tube

Is this just an identified portion of a fluid (a dense gas or a liquid), or is this plane of molecules the only thing in the tube? This makes a difference.

What makes those 3 molecules so special ?

If the molecules are otherwise alone, those are the molecules that interacted with the walls and were slowed down by the normal reflection being directed inward.

If the molecules are part of a fluid, it makes no sense to think of the molecules as being able to stay in a plane. The intermolecular forces will jumble them quickly, even if the tube were perfectly parallel. The random motion will move some ahead and some behind. As the fluid moves to the smaller cross section, the pressure gradient will cause an acceleration gradient. The ones most in front will be random based on interactions within the fluid.

Answer 4

The initially introduced 30 molecules all occupying a 2D flat crossection plane of this reverse acoustic waveguide at its entry open end, cannot remain in the same plane since our waveguide towards the direction of propagation closes up and there will be a pressure gradient meaning the molecules will non-uniformly speed up (Bernoulli) with the molecules positioned each time closer to the center of the waveguide and experiencing higher pressure to get the highest velocity boost. The plane of molecules will be translated into a "bullet" formation passing though this narrowing waveguide.