0

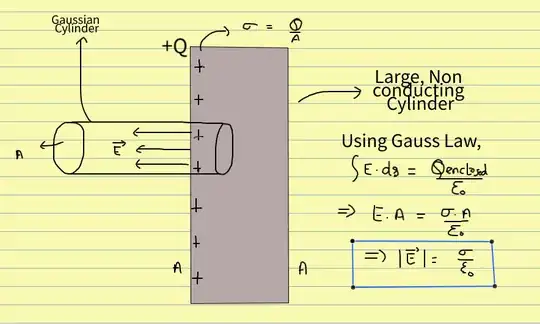
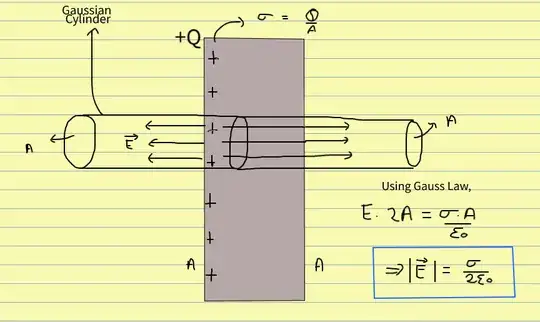
I'm trying to derive the electric field due to a single large, thin, non-conducting plate at a point (see figure). I'm solving it using 2 methods, and arriving at a different answer using both.

I've referred some textbooks, and they say that the result of the 2nd derivation is correct. I would like to know which method is correct, and why is the other method wrong? Can I change any equation/assumption in the wrong method to arrive at the right result?

Derivation 1:

Derivation 2:

enter image description here

Images produced by myself using this website.

BlazeRod11
  • 19

2 Answers2

0

The first derivation is incorrect because we assume the sheet of charge to be infinitely thin and the surface you are using to apply Gauss Law is also infinitely thin, and so the Gaussian surface must either contain the charged sheet (as it does in derivation 2), or it doesn't contain the second sheet, in which case $Q_{enc}=0$ and so Gauss Law doesn't do anything for us, since we just get $0=0$.

As you mention in the question the second derivation is what gives us the correct answer for Electric Field due to this large-thin sheet, and is how its done in most all textbooks.

xXx_69_SWAG_69_xXx
  • 1,808
0

Since it's a nonconducting plate, the charge sits only on the left surface and there is indeed an electric field inside the material (we're ignoring dielectric effects here, right? otherwise you'll need to know the dielectric constant of the material.) So I would say that your mistake is that you did NOT draw the electric field going to the right inside the material in your first figure (Derivation 1). You can keep the Gaussian surface inside the material, but there IS an electric field in there, just as you've drawn in the Derivation 2. The charge enclosed is the same in both pictures, and the flux is 2EA in both pictures.

Note also that if this were a conductor, then the electric field would be zero inside the material and Derivation 1 gives the correct answer. Of course, if it were a conductor, then there must be an equal amount of charge on the right surface of the conducting plate. This would give E = 0 inside, and $E = \sigma/\epsilon_0$ outside

quantumwave
  • 531