Deriving speed of waves equation

Question

I am trying to derive the speed of a wave equation $$v = \sqrt{F/\mu}$$ starting from a segment of string under tension with a force of $F$ in which a pulse moves with a speed of $v$. Can someone show me how to derive this equation?

Answer 1

I think most textbooks will show the derivations. Here I am going to show 2 methods from the book physics for scientist and engineers by Serway and Jewett. It is actually quite a nice book. If you are interested in general physics, I think you should read it.

First method : Change the reference frame

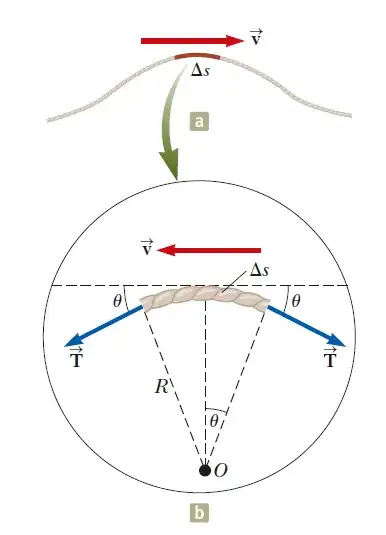
For the first method, we will analyse the top part of a pulse in a wave (with velocity $v$ to the right), as shown by $\Delta s$ in figure 1(a).

Now, before analysing the force on the $\Delta s$, we need to consider an appropriate frame of reference that can simplify our derivation.

The ground frame is actually not good enough, as the individual points on the string will only move vertically, and it is hard for us to find the relation between the force and the velocity of the wave (which is horizontal).

Here is the genius point: let us consider another inertial frame with velocity $v$ relative to the ground frame.(i.e. we will be at rest compared to the wave )

On one side, by changing the inertial reference frame, we will not change the force and acceleration, on the other side, the individual points on the string will now move from right to left with velocity $v$, while the shape of the wave will be at rest, shown in the figure 1(b) (I think you can imagine that the string is now like a stream of water, flowing from right to left while tracking the same shape of a pulse just in front of you. )

Since the $\Delta s$ part is almost flat and we can actually consider it to be an arc of a circle with radius R. Thus, $\Delta s$ is in a circular motion and its mass is $\mu \Delta s$. The net force on it will thus satisfy (using the relation between centripetal acceleration and velocity):

$$ \begin{align} \sum F &= m\frac{v^2}{R}\\ &=\frac{ \mu \Delta s v^2}{R} \tag{1} \end{align} $$

Notice, as $\Delta s$ is now considered an arc, it will satisfy the arc length formula, i.e. $\Delta s= 2R\theta $

(1) will then be $$ \sum F = 2\mu \theta v^2 \tag{2} $$

Don't forget that the forces on $\Delta s$ are tensions provided by other parts of the string. The horizontal part will cancel out as we consider $\Delta s$ to be symmetrical. Hence, we also have,

$$ \sum F = 2T\sin\theta \tag{3} $$

Sub (3) into (2), use small-angle approximation (as $\Delta s$ is flat, $\sin \theta \approx \theta$), we have $$ T = \mu v^2 $$

Ta-da! We are done.

This is the first method and the idea of changing reference is quite interesting.

================================

Second method: the wave equation

The second method will consider the 1-D wave equation. Personally, I find it more rigorous.

Firstly, we define wave to be some displacement functions $u(x,t)$ which only translate its shape through space and time. $$ u(x,t) = f(x\pm vt) $$ Then, we can derive the wave equation (for details of working, you can check this question Derivation of 1D wave equation) $$ \frac{\partial^2 u}{\partial x^2} = \frac{1}{v^2}\frac{\partial^2 u}{\partial t^2 } $$

for convenience purpose, we use $u_{xx}$ to denote $\frac{\partial^2 u}{\partial x^2}$ and $u_{tt}$ to denote $\frac{\partial^2 u}{\partial t^2 }$. Same for $u_x$ and $u_t$.

Now, let us try to give these second partial derivative some physical meanings.

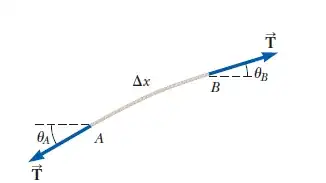
Consider another small length of string $\Delta x$ in the string, which make a small angle $\theta_A$ and $\theta_B$ with the horizon.

The vertical net force $\sum F = T (\sin \theta_B - \sin \theta_A)$ As the angles are small, we can use small-angle approximation. $\sum F = T(\tan \theta_B - \tan \theta_A)$.

From maths, we know that $\tan \theta= \frac{\partial u}{\partial x}$ (I think this is also the origin for the name "tangent" which appear in both trigonometry and calculus)

Thus, $$ \sum F = T(u_x(B) - u_x(A)) \tag{4} $$ where $u_x(A)$ means the partial derivative at point A.

At the same time, net vertical force provides the vertical acceleration, i.e. $$ \sum F = \mu \Delta x a $$

The acceleration here will just be the second derivative of displacement about time, i.e. $u_{tt}$.

Thus, sub this into (4), we see $$ T(u_x(B) - u_x(A)) = \mu \Delta x u_{tt} \tag{5} $$

By definition, $$ u_{xx} = \lim_{\Delta x \rightarrow 0 } \frac{u_x(B) - u_x(A)}{\Delta x } $$

Hence, from (5), we can get $$ Tu_{xx} = \mu u_{tt} $$

Recall wave equation $$ v^2u_{xx} = u_{tt} $$

Finally, we can see that $$ v= \sqrt{\frac{T}{\mu}} $$

So, these are the 2 methods for wave speed. Hope the explanation is clear and helpful.

Answer 2

The equation is fairly simple in that it can be determined (up to a constant of proportionality) using dimensional analysis. Given the dimensions of $v$, $F$, and $\mu$, you can work out what the relationship must be between $F$ and $\mu$ in order that they produce the dimensions of $\mathrm{Length \, over \, time}$.

The constant factor can then be determined via experiment.