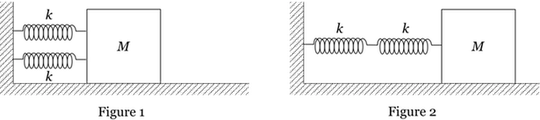
Two identical springs with spring constant $k$ are connected to identical masses of mass $M$, as shown in the figures above. The ratio of the period for the springs connected in parallel (Figure 1) to the period for the springs connected in the series (Figure 2) is $ 1/2 $
What would be the better way to solve this? I have used this law $$\begin{equation} T = 2 \pi \sqrt{\frac{l}{g}} \end{equation}$$ and assumed, $2l$ for the $2^{nd}$ picture but got wrong answer.
Two springs in parallel effectively behave as a single spring with spring constant $k_\mathrm{parallel} = k_1+k_2 = 2k$ while two springs in series effectively behave as a single spring with spring constant $k_\mathrm{series} = k_1k_2/(k_1+k_2) = k/2$. Recall that the period of a mass on a spring is $$ T = 2\pi \sqrt{\frac{m}{k}} $$ Which gives $$ \frac{T_\mathrm{parallel}}{T_\mathrm{series}} = \sqrt{\frac{k_\mathrm{series}}{k_\mathrm{parallel}}} = \sqrt{\frac{k/2}{2k}} = \frac{1}{2} $$
You are using the wrong law .
This is linear SHM. Find out the time period for that , it will be $2\pi \sqrt \frac{m}{k}$
.
Then figure 1 , springs are in parallel and in figure 2 , springs are in series . Do a wiki search to figure out how to find equivalent springs .
An Advice : Don't learn equations blindly .