Why doesn't the voltage increase when batteries are connected in parallel?

Question

Can you please explain the thing below?

When we add a battery in circuit then, it gives out some electric field that moves through the circuit and gives a force on electrons in conductor to produce current.

When we connect two batteries parallel with each other in a circuit then the electric fields coming out of both batteries moves through the conductor which should give more flux than before. As there is the double number of fields in the same area. But the voltage doesn't double.

What have I done wrong here?

Are there any increasing flux/electric field magnitude when two batteries are connected parallel in a series?

New Edit: I think I have a got three of the very close answers. Let us think about what is going on on the positive terminal and then we will apply the same to the negative terminals just to make it easy to understand.

1. "Because the batteries were originally designed for V volts. But on adding batteries in parallel makes a large amount of repulsion in positive terminals that is felt by both batteries and reduces the amount of charge on each terminal which also decreases the voltage of each battery. The total charge of both positive terminals is the same as we get when using battery."

2. "But there are people also saying that it depends on concentration of charge not amount of charge"

3. "The one another explanation was: first assume that E is the electric field released by each battery, that half of electric field(E/2) from one positive terminal moves toward another positive terminal therefore reducing its half strength and the another half field (E/2) moves in the circuit (not toward the positive terminal) to increase the strength by (E/2), therefore making the total electric in through the resistor = E "

Answer 1

tl;dr Batteries do not create electric fields to move charges. They move charges, which creates electric fields.

a battery [...] gives out some electric field that moves through the circuit and gives a force on electrons in conductor to produce current.

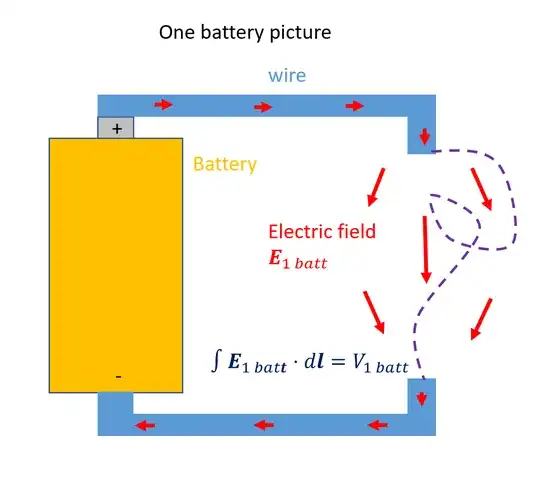
This description is, if not completely wrong, at least misleading. A battery is not a source of electric field, it is a source of electric potential. Imagine a battery with terminals in the shape of a pair of parallel conductive plates with an air gap in between (this is a capacitor): as you move the plates toward each other, the field strength (between the plates) increases, and as you pull them apart, the field strength decreases. There is no upper limit to how strong the field can be (well, until it reaches the breakdown voltage and begins to arc), and no lower limit either -- the strength of the field is not determined by the battery. So the battery itself does not directly create an electric field between its terminals.

Moreover, electric field does not "move through" a circuit; charges do. In a simple DC setup like a battery driving current through a resistor, all electric fields are stable over time -- the charges move through the circuit, but the field itself does not. Saying that electric field moves through a circuit is a bit like saying that gravity moves through a rollercoaster. Moving electric fields do come into play with AC circuits and devices with moving parts, such as electric motors; but even a non-moving electric field causes charges to move through a conductor (this is, after all, essentially the definition of "conductor").

So how does current work? Batteries are a source of electric potential, which is measured in volts. Potential is a kind of pressure and in a typical battery this pressure is caused by chemical reactions inside the battery pumping electrons from one terminal (+) to the opposite one (-). The potential difference between the terminals does create an electric field. In the experiment above where the terminals of the battery are parallel flat plates separated by a distance $d$, you could calculate the field strength between them as simply $E = {V \over d}$. But the field is just a way of observing the potential difference between the terminals: it's not the reason the charges are moving in the first place (which is, again, the chemical reactions happening inside the battery).

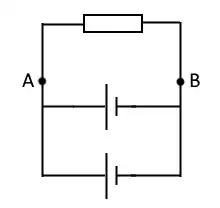
Pressure is relative, and electric potential is no different. To be strictly accurate, what a battery provides is an electric potential difference ("voltage") between its two terminals. This is basically a measurement of how strong an electron-pump the battery has inside it. This is why connecting two identical batteries in parallel does not add their voltages: because they both provide the same potential difference between the (+) and (-) terminals, there is essentially no difference between two batteries connected in parallel and two isolated, disconnected batteries. The electric potential between the (+) terminals and (-) terminals is the same, and both batteries "agree" on it, so there is no reason for current to flow between them. (Connecting two mismatched batteries in parallel will cause current to flow, in a direction determined by which battery has higher voltage.)

What connecting two batteries in parallel does do is change how the system behaves when under load. If you connect a load, say a 1kΩ resistor, across the terminals of a single 1.5-volt battery, the current through the resistor will be 1.5 mA, all of which is supplied by the same battery. If you connect the same load across the terminals of two 1.5-volt batteries connected in parallel, the current through the resistor will still be 1.5 mA, but now each battery only has to supply 0.75 mA of current. This means that each individual battery is under less load than before, because the electrochemical pumps inside it only have to move half as many electrons to maintain the same voltage. These batteries may last longer and behave better under a variety of loading conditions. (This assumes ideal conditions and perfectly matched batteries. In real-world scenarios, batteries are never perfectly matched, and so you may need a load-balancing circuit to protect the batteries from each other.)

Answer 2

Think of a battery as an escalator (potential gravitational energy and potential electric energy/voltage are analogous here).

If you have two escalators side by side, taking either one will get you to the same height. If you have two escalators in a row, you will have to take them both and therefore get twice as high. The advantage of escalators side by side is that it's less taxing on their engines.

A battery raises the voltage in a wire by a set amount. Two batteries in series will raise the voltage twice as high, two batteries in parallel will make the batteries last twice as long.

---

Edit: OP has asked for an explanation without an analogy. A battery will raise the voltage of a current by a set amount. This is why we have things called "12 volt batteries" and not "12 newtons/coloumb batteries". If a current is at 0 V when it splits into parallel and goes into two separate batteries, then the electrons in each circuit will go up 12 V, then join back together at exact 12 V. If you have the batteries in series, the electrons will go from 0 to 12 after the first battery, then 12 V to 24 V through the second battery.

You mention E-field flux as being a sticking point for you - but E field flux doesn't define potential. And incidentally, the E field flux through each separate wire in parallel will be identical. The E field flux through the wire in series will be double what one wire would be in parallel.

Answer 3

Since you seem to be eager for an analogy-free answer, I'll try to give it a stab. I think this question is actually a bit deeper than some of the answers are giving it credit for, and so far I think trentcl answers your question the best: the root cause of your confusion is that you are assuming that batteries act as sources of fixed fields, rather than fixed potentials. But I'll try to go into a bit more detail as to why that is.

Now, your question seems to more or less be the following: say I have a battery, with some wires attached to it, like in the diagram below. In general, there will be some wonky electric field generated between the two leads whose structure is dictated by maxwell's equations. However, since everything about this problem is static, we know that if we integrate the electric field over any path between the leads, we will get the same voltage-- and it's this voltage that can do work if we put some lumped element device like a resistor between the leads.

Now, to the meat of your question. As we all learn, Maxwell's equations are linear-- we can take any solution and add the fields and we'll have another solution. So if we take another battery and attach the leads to the first, we should generate roughly twice the fields between the leads and hence twice the voltage, right? Wrong.

The problem is that you're ignoring the mechanics of the battery. Batteries work via chemical reactions that preferentially move charge in a certain direction, and they only push these charges so hard. When you start linking up batteries in parallel, the fields generated from one battery push back the charges from the other until you end up with an equilibrated system where the potential between the leads is the same as it was for a single battery.

So in fact, how a battery works is affected by presence of electric fields and it turns out you can't just superimpose the fields from two batteries when you connect them in parallel. Maxwell's equations are linear, but when you couple them to matter in a multiple particle system (like that of a battery) they aren't-- a simple example is a single electron will travel in a straight line, whereas if you have two of them initially side by side they will curve towards each other.

Now in reality no one every takes this "force-like" approach of looking at dynamics of batteries-- it's just too complicated and turns out to be pointless anyway. A much better approach is an "energy-like" approach. Each individual chemical reaction inside the battery only produces so much energy, and you can get pretty far by just keeping tabs on this. Since voltage is basically a measure of potential energy, when you do this it's pretty easy to argue that batteries (barring extreme conditions) should act as constant voltage sources, rather than constant electric field sources. But it helps to play around in the muck of a force based approach first to get a more intuitive explanation of what's going on.

Answer 4

If a battery is defined as a device that maintains a constant voltage across its ends, then automatically the problem is solved. When connected in series each battery maintains that constant voltage across its ends and hence they add up. But If connected in parallel, they remain the same by definition.

But this is not an answer unless I explain why the voltage across the ends of a battery remain same.

And for that we need to look inside a battery.

Inside a battery are two Chambers : one which loves to lose electrons and another which loves to gain electrons. And the eagerness to lose or gain electrons is dependent on the concentration of reactants inside each chamber. A more precise statement : Energy gained in moving a charge from one chamber to the other ($~$ voltage) is dependent on the concentration.

The Chambers are as shown in fig 1. When we make a circuit, we are connecting these Chambers together. Electron flows through the external circuit under the potential difference.

when connected in parallel as you can see from figure, nothing has changed. Two parallel connected chambers is equivalent to the each chamber just becoming large. We now have more chemicals in the cell, but concentration is the same. So the voltage, which we may define as the energy gained in moving a charge from one chamber to the to the other, remains same.

when connected in series
I hope it is clear already... concentration is still the same. each battery maintains its voltage across it. So total voltage it the sum of individual voltages.

Answer 5

Think of this in the water analogy. Wires are represented by canals, the height of the water level is the voltage and the flow rate is the current. A battery, by definition, raises the voltage on one of its terminals by a set amount compared to its other terminal. So in the water analogy it's like a pump that keeps the water level on one end 2 meters higher than at the other end. Here 2 meters is just an arbritary number.

If you connect two batteries in parallel at some point you have to create a junction where 3 wires meet. Any two points in a circuit that are connected by a wire without a resistor in between are at the same voltage. So each of the 3 wires connected to the junction are at the same voltage. In the picture below every part of the wire that is touching point $A$ is at the same voltage and similarly any wire directly connected to point $B$ is at the same voltage. The voltage difference between $A$ and $B$ can be seen as the output voltage of the two batteries combined so that's why the voltage doesn't increase when you combine batteries in parallel.

To see why every part of the wire is at the same voltage we can look at the water analogy. Connecting two wires together is like joining two canals together. If the water level in one of the canals was higher than the other before joining then as soon as they are joined water will start rushing to the part with the lower water level. After everything has settled you are left with one big canal with a water level that's the same everywhere. You can have a voltage difference over components like resistors or batteries. Resistors are comparable to dams which let a small amount of water through and which can have different water levels on either side of it.

Remember that this 'settling' which I mentioned happens extremely quickly in electrical circuits. In water circuits you would be able to see the water settle but in electrical circuit this happens almost instantaneously.

So finally you might ask why is voltage so similar to water height? Voltage is the energy (per charge) in a circuit. So if any part of a wire has a higher voltage than its surroundings it will generate an electric field. This electric field will always act in such a way to rearrange the charges in the wire until the voltage is completely uniform. Similarly to how a higher water level means more potential energy for the water.

Answer 6

OK, there are a lot of answers here, but they're all long, I don't really like any of them, and the answer is simple, so here's another one...

All by itself in space, a battery will push electrons from its positive terminal to its negative terminal. This will create a field such that moving an electron along any path from its positive to its negative terminal will take 1.5eV of energy (approx, assuming a 1.5V battery).

If you put two of these batteries next to each other, their fields interact, and some of the electrons on their negative terminals will be forced back inside and some will come back out on their positive terminals. The electrons redistribute and change their fields to ensure that it still takes 1.5eV of energy to move an electron from a battery's positive terminal to its negative terminal.

If you actually connect these batteries in parallel, the electrons redistribute again, and now it takes 1.5eV of energy to move an electron from anywhere on the common positive wire to anywhere on the common negative wire.

Answer 7

Each electron is individually pulled (randomly?) from the lower potential terminal (negative terminal of the anode) of one of the two batteries and works its way through the load device to ultimately return to the higher potential terminal (positive terminal of the cathode) of the same battery. (The positive and negative signs of the terminals refer to their relative voltages, NOT their charge.)

The electron has to return to the same battery to maintain charge neutrality and current continuity everywhere in the circuit and the battery. Each loop occurs independent of the other battery as the two batteries are in parallel. Also remember that the definition of a battery is an assembly of materials that maintains a constant voltage difference between the two terminals.

The voltage difference between the terminals of any battery arises from a thermodynamic tug-of-war for electrons between the chemicals of the two electrodes. The cathode wins the tug of war by pulling electrons from the anode, via wires in the load device. The voltage difference between the terminals is the work to move one electron from low voltage to high voltage (or one conventional positive charge from high voltage to low voltage). To maintain charge neutrality there is a form of counter-current salt bridge inside the battery.

You could also consider 2 different sized 1.5 v batteries, such as AAA vs D with the same chemistry. In a sense, the D cell functions as an array of AAA batteries in parallel. The D cell battery stores more total energy (mA hr) than the AAA because it contains a greater mass of chemicals at the anode and cathode, and thus it will last longer than the AAA when the same current is drawn from both. But they are the same voltage.

(If the batteries were connected in series, it would be different because now each electron is being passed through both batteries, so the voltages do add up. This is what happens inside a 9V battery, which actually contains 6 AAAA 1.5 V batteries in series.)

Answer 8

Internally a battery cell creates a fixed voltage potential between the positive and negative sides. So a 5 V cell would have a five volt difference between the positive and negative end of the cell.

When you put two batteries in series, we generally call the negative end of the first cell 0 by convention. The positive end of the first battery then has +5 V. Since the positive end is attached to the negative end of the second, it too will be at +5 V. Since the positive end of the second is 5 V above the negative end (now at +5 V), it is now at +10 V.

Compare to two batteries in parallel. The negative ends of the batteries are connected, so both are at 0 (again, by convention). For the first battery, we get 5 V above the negative end (0 V) for a total of +5 V at the positive end. For the second battery, we also get 5 V above the negative end (0 V) for a total of +5 V at the positive end.

You might notice that there seems to a contradiction if the batteries are of different voltages, for example 5 V and 8 V. The negative ends touch so are the same at 0 V, but the positive ends touch and are different at 5 V and 8 V. In reality there will be some internal resistance so there will be some increasing potential as you move along the wires connecting the batteries (this charges the 5 V battery by the way). In general though, this resistance is small enough to ignore.

Answer 9

Batteries are voltage sources that use chemical reactions to provide an electromotive force — that is, a force applied to electric charges (e.g. electrons) that results in the increase of electric potential energy of those charges. This is what results in an electric potential difference across the battery — that is, electrons at the positive terminal have less electric potential energy than electrons at the negative terminal. The difference in potential energy (measured in joules) per unit of electric charge (measured in coulombs) is called the electric potential difference. It is measured in volts (equivalent to joules per coulomb), hence the equivalent term voltage.

Crucially, when batteries are placed in series, electrons will necessarily move through one battery, acquiring some electric potential energy, and then through the second battery, acquiring more electric potential energy. However, when the batteries are instead placed in parallel, electrons will only move through one of the two batteries — not both — and thus the total amount of electric potential energy acquired by each electron is less. Specifically, in the case of the two batteries having equal voltage, having the batteries in series will result in the electrons each acquiring twice as much electric potential energy as they would if the batteries were in parallel or if only one of the batteries were present.

Answer 10

I will try to explain in 1000 words.

Let B = Battery

B+B = 2B,

but it doesn't happen like that with electric potentials. There is more to it. Assume 2 batteries as railguns, with total available energy 2E and the electron as a bullet. The railgun shoots electrons with velocity V.

But if railguns are connected in series, the velocity of the electron will not be 2V, but instead √2V since energy is doubled. And in series N electrons can be shot, since 2 units of energy is expended to increase the electron velocity.

In the case of railguns connected in parallel, 2N electrons with velocity V can be shot, therefore the amount of electrons is doubled compared to a series, as only 1 unit of energy is expended on an electron by the time the electron leaves the gun.

This constant flow rate of electrons is due to the constant current nature of electro-chemical batteries, since X molar equivalent of cathode and anode must redox to produce electricity, and the rate of reaction remains fairly constant.

Key terms: railgun is nothing but a coil, a long electromagnetic coil-like particle accelerator. Battery is your regular AA battery (example dur@cell). We will not assume power supplies as their nature is different, and we do not connect power supplies in series!

Answer 11

There is so much good theory here already that I'll just add simple analogy, which is actually decent, because we're still talking about potential, which is only a function of position – not path. As voltage is a function of two points regardless of path (let's assume there are no changing magnetic fields here for simplicity), having another path available changes nothing.

If you're on top of a hill, do you expect stuff to roll down faster and gain more energy just because there's another alternate slope down (that you're not using) in some other direction, which nevertheless ends at the same altitude?

Answer 12

Look at two opposite charges at a fixed distance from each other. The electric field around them is expressed as Volt per meter ($\frac{V}{m}$). Or Newton per unit charge ($\frac{N}{C}$), where a unit charge refers to a test charge being put in the field.

So say these charges constitute a battery (though when being rigorous, the total field of a battery is not the same as a dipole, but the outside field is):

The battery poles contain many charges, so the electric field will be much higher than that of two single charges (as depicted in the previous picture). If there are twice as many charges on the poles of the battery the field will become twice as big, as will the voltage (because the field is defined as Volt per meter as well as Newton per unit charge). If the two batteries are placed parallel in the circuit the electric field surrounding the batteries will indeed add up. But the field at the poles will stay the same (except if the poles coincide in which case you have a new battery of higher voltage). The voltage of a battery is the voltage between the poles. This voltage is sent into the wires. So while the surrounding field can increase, the field inside the wires is that of the poles. When you place a loose wire around the batteries, initially the superimposed field of both batteries will be present (which is higher than the field at the poles), after which a contra field is built up by the charges inside the wire which cancels the field of the batteries). If the poles coincide (which is not the case when the batteries are placed parallel) you have a new battery of higher voltage. This is achieved by placing two batteries in series in which case the charges on the poles which you connect to the circuit will be doubled.

In short: while the field surrounding the parallel batteries increases it is the field on the poles that matters. This field is sent into the circuit and not the field at a distance from the poles (which is indeed the sum of the fields of both batteries). The field inside the wires is that of an individual pole, not that of both added. This field will last longer because the parallel batteries contain more electrons than one single battery. That is, the parallel batteries have more capacity and the same voltage. Now you might think that if both poles send the same field into the circuit why will the field in the circuit not be twice that on the poles? This would only be the case though if the plus poles of the parallel batteries coincided as well as the minus poles (and the charges on the poles would stay the same) which means that you would have a new battery of higher voltage.
Likewise, if you place two batteries in series, the field on the poles that are connected to the circuit is the sum of the fields of the two individual batteries. That field is sent into the circuit. There are twice as many charges on the poles connected to the circuit. That is the voltage of the batteries in series is the sum of the individual batteries.