I am very much a physics novice, and am currently taking Physics C in high school, but we've discussed the Maxwell Faraday equation, and I had a question about it.
To be more clear, the maxwell faraday equation we are dealing with is in its integral form:
$$
\oint_C E\cdot dl=-\frac{d\Phi_B}{dt}
$$
And this I have an understanding of. But my question lies in more complicated surfaces. I have an interest in topology, and my, again, novice understanding of topology makes me think that the closed loop wire $C$ that this equation is working on only really works if the wire in question has a Seifert Surface that is orientable. My question is, what happens if the Seifert Surface is non-orientable? Such as a trefoil knot of a wire with a $B$ field "perpendicular" to it? Diagram below.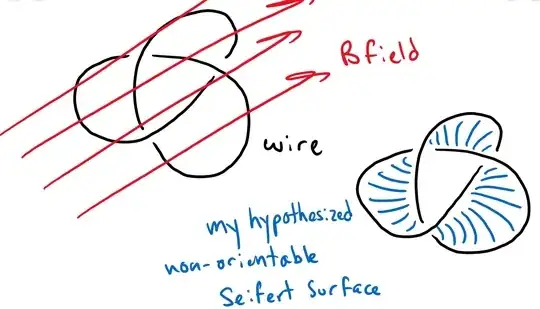
So if anyone knows what happens in this scenario, whether there is no current in the loop, or whatnot, I would appreciate any clarification. Thank you!