If particles can find themselves spontaneously arranged, isn't entropy actually decreasing?

Question

Take a box of gas particles. At $t = 0$, the distribution of particles is homogeneous. There is a small probability that at $t = 1$, all particles go to the left side of the box. In this case, entropy is decreasing. However, it is a general principle is that entropy always increases. So, where is the problem please?

Answer 1

Right, there is a small probability that the entropy will decrease. But for the decrease by $-|\Delta S|$, the probability is of the order $\exp(-|\Delta S| / k)$, exponentially small, where $k$ is (in the SI units) the tiny Boltzmann constant. So whenever $|\Delta S|$ is macroscopically large, something like one joule per kelvin, the probability of the decrease is de facto zero.

If you have $10^{20}$ molecules of gas (which is still just a small fraction of a gram), the probability that all of them will be in the same half of a box is something like $2^{-10^{20}}$. That's so small that even if you try to repeat the experiment everywhere in the Universe for its whole lifetime, you have no chance to succeed.

Statistical physics talks about probabilities and quantities with noise, as the previous paragraph exemplifies. But there is a limit of statistical physics that was known earlier, thermodynamics. Effectively, we can say that thermodynamics is the $k\to 0$ limit of statistical physics. We just neglect that $k$ is nonzero – it is tiny, anyway. In this limit, the noise of different quantities disappears and the exponential $\exp(-|\Delta S| / k)$ is strictly zero and the decreasing-entropy processes (by any finite amount, in everyday SI-like units) become strictly prohibited.

Answer 2

Even though the answer you chose is very good I will add my POV

Take a box of gas particles. At $t=0$, the distribution of particles is homogeneous. There is a small probability that at $t=1$, all particles go to the left side of the box. In this case, entropy is decreasing.

Take the statistical mechanics definition of entropy:

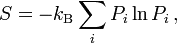
where $k_B$ is the Boltzmann constant .The summation is over all the possible microstates of the system, and $P_i$ is the probability that the system is in the $i$th microstate.

The problem is that this one system you are postulating in your question is one microstate in the sum that defines the entropy of the system. A microstate does not have an entropy by itself, in a similar way that you cannot measure the kinetic energy of one molecule and extrapolate it to a temperature for the ensemble of molecules.

An observation on systems with decreased entropy: Entropy increases in a closed system. If an appropriate liquid is turned into a crystal, the ensemble of molecules will have lower entropy, but energy will have been released in the form of radiation, the system is closed only when the radiation is taken into account for the entropy budget.

Answer 3

Statistical physics doesn't tell you that entropy will increase all the time. Just that it will increase on average.

The maximum-entropy state is the one with the largest number of microstates. This doesn't prevent you from observing an odd state every once in a while -- even one with very low probability -- in fact fluctuations of the state do happen and are measurable. These fluctuations are centered about a state called equilibrium -- but if entropy could only strictly increase these fluctuations would not happen in the first place. Every isolated state would be stuck in equilibrium forever.

To elaborate on the point about averages -- the state which maximizes the entropy has the highest probability -- which is itself an average.

So for any moment in time our world is exceedingly more likely to increase its entropy than it is to decrease it, but there is no law, besides the law of large numbers, that prevents it from going the other way.

Answer 4

Think of entropy as a steady-state quantity related to system dynamics: Wait for a 'long time', smear out the phase space trajectories and measure the resulting volume.

This means that even if all gas particles ended up on the left side of the box (unlikely, but not impossible and realized by perfectly valid microstates), entropy only would have decreased if they stayed there and never expanded to fill the whole volume again (which is even less likely and assumed to be impossible under the fundamental assumption of thermodynamics).

---

Note that even though the situation (all gas particles moving to the left side of the box) looks vastly different from the idealized equilibrium picture (think about what happens to pressure!), this is perfectly fine as thermodynamic variables are subject to random fluctuations, which can be large (but probably won't be).

This is essentially the same point (or rather one of the points) the accepted answer makes if you replace ensemble averages by time averages - I just prefer the dynamic picture I painted here:

Physics isn't really about abstract ensembles, information and missing knowledge - it's about energy, activity and variability: If you prayed to god and 'e felt generous and shared the knowledge about a particular thermodynamic system with you, that knowledge would not have any effect on your measurements. Dynamics place limits on relevant knowledge, but knowledge doesn't cause dynamics.

Also, as far as I'm aware, Luboš comments are misleading: Non-equilibrium thermodynamics is still largely an open problem, and the thermodynamic definition of entropy explicitly depends on equilibrium, regardless if you use the traditional definition based on Clausius' 19th century analysis or prefer a more axiomatic treatment.

Answer 5

There is a certain amount of confusion about what is the difference between a macro-state and a micro-state.

Formally, a micro-state is the complete specification of all physical properties of the system: the complete location and momentum of each individual molecule. A macro-state, formally, can be any set of micro-states. Even more generally, and this is the setting of the formula, due to Gibbs, which anna v has written, a macro-state can be any probability distribution of micro-states, i.e., any collection of micro-states $i$ together with a coefficient $p_i$ for each micro-state, the coefficients are "probabilities", whatever that means, so they havbe to be positive real numbers that add to one. Boltzmann, and us too from now on, will simplify life and assume that all micro-states have equal likelihood, and even we will make the $p_i$ all equal to unity. (He has been criticised for this but it works.)

Strictly speaking, only macro-states have entropy. The entire ensemble is a macro-state, it is the set of all possible micro-states. But it is not the only macro-state. For $A$ any set of micro-states, let $\Omega$ be the number of micro-states in it. Boltzmann's definition of its entropy is $$S = k \log \Omega.$$

Nothing goes wrong with StatMech if you stick to this formalism, but there is supposed to be a physical intuition behind this distinction. Different people make different points here, but what we can use is this intuition:

a macro-state should be a collection of all the micro-states which are macroscopically indistinguishable from each other in some respect.

Now the OP asked about when all the molecules are in the left side. This is almost a macro-state. But not quite. But let us say A means "99.99% of the molecules are in the left side". This can be detected macroscopically, and if there are about $10^{23}$ molecules, and if each one has only about $7^{103}$ different ways to be "on the left side", then there are something like ... well, this is left as an exercise... there are a lot of ways that .01% of them can be on the right side, but this is still way, way less than the number of different ways for "50% plus or minus 0.01% to be on the left, and the rest on the other side". The entropy of these two macro-states will be vastly different. The macro-state which anna v has in mind is the macro-state of all micro-states, but that macro-state is not the only one that can be studied. The OP would not be far off thinking of the micro-state "all particles on the left" as if it were a macro-state and calculating its entropy to be zero. IN comparison to the entropy of the other macro-states, it is zero.

The OP started by talking about a homogeneous distribution of positions (and presumably momenta obeying the Maxwell distribution) of the particles at time t = 0. This is also a macro-state, call it B. There are a truly vast number of different micro-states all of which obey this description. Overwhelmingly more than the number in the macro-state A. So it has its own entropy, too. It is, however, more or less certain that one of these micro-states in B really will evolve to be a micro-state in A. But the probability of this happening is as small as Prof. Motl says it is.

See Sir James Jeans's discussion of a fire making a kettle of water freeze, which I posted as part of an answer to a similar question, Does entropy really always increase (or stay the same)?