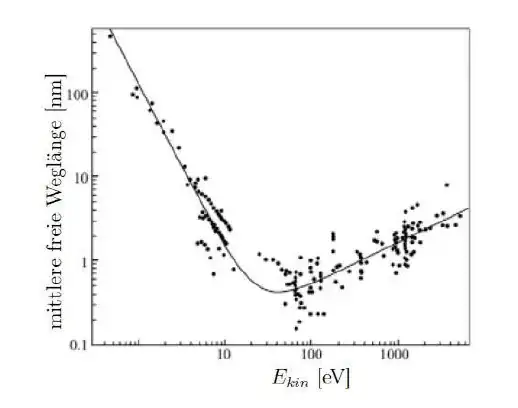
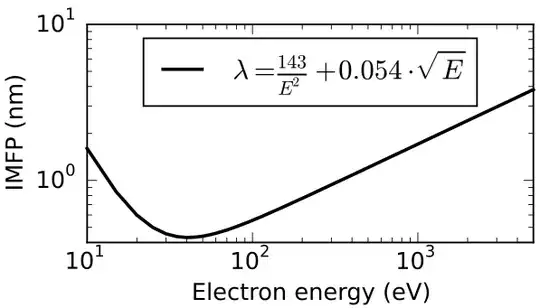
- Why does the mean free path length have a minimum, or rather why does it increase at lower energies?
First, it is important to realize that the plot (the plot at the bottom of the updated/bountied question) is illustrating the inelastic mean free path for electronic scattering. It doesn't take other types of scattering into account, such as the scattering of electrons from phonons.
Because we are only considering electronic scattering, the most important energy scale in a solid is characterized roughly by the "plasma frequency," which for many solids is on the order of tens of eV. Of course, in a real solid there is no single "plasma frequency," but nevertheless the electronic absorption does usually have a strong peak near some tens of eV.
The "plasma frequency" can be used to make some very simple models of the electronic response of a solid. For example, the dielectric function can sometime be usefully approximated simply as:
$$
\frac{1}{\epsilon(\omega)} \approx 1 + \frac{\omega_P^2}{\omega^2-\omega_P^2+i\omega\delta}\;,\tag{1}
$$
where $\omega_P$ is the plasma frequency and $\delta$ is a small (or infinitesimal) constant. The imaginary part of the dielectric function, in this approximation, is strongly peaked at $\omega_P$. Of course, in real life the dielectric function is much more complicated, but the imaginary part still tends to have peak in the tens of eVs.
Why am I even discussing the dielectric function here? Because it turns out that the linear response of the material/solid (characterized by the solid's dielectric function) is very important when describing electronic stopping power and inelastic mean free path.
For example, the inelastic mean free path is calculated as an integral involving the dielectric function:
$$
\frac{1}{\lambda(E)} = n\sigma = n\int d\omega \frac{d\sigma}{d\omega}\tag{2}
$$
$$
= n\int dq d\omega \frac{d\sigma}{dq d\omega}
\sim
\alpha\int dq d\omega Im\left(\frac{1}{q\epsilon(q,\omega)}\right)\;,
$$
where $\sigma$ is the inelastic scattering cross section, and where $\alpha$ is a constant, and where $n$ is the number density of scatterers and $v$ is the electron's velocity. (I'm using the $\sim$ symbol in the last line since there is a transverse part of the cross-section I am neglecting.)
N.b., Equation (2) follows from the definition of the mean free path $\lambda$ (and mean free time $\tau$):
$$
1= n\sigma v\tau = n \sigma \lambda\;.
$$
This definition is reasonable, since it follows from considering how many collisions would occur as a particle with cross-section $\sigma$ traverses a medium with scatterers of number density $n$. As the particle moves, it sweeps out a tube of volume $\sigma v \delta t$, thus the number of collisions is: $N=\sigma v\delta t n$. The definitions of $\tau$ and $\lambda$ follow by setting $N=1$.
N.b., the definition of the mean free path hinges on what exactly we mean by the "cross section." In this case we consider the inelastic scattering cross section, so we could more accurately characterize the "mean free path" as the "mean free path for inelastic scattering."
Once the energy of the scattering electron is below the plasma frequency it is hard to make electronic excitations. This is why the mean free path for inelastic scattering goes up at low energies. (Where "low" means low compared to the plasma frequency.)
Alternatively, you can also think of the inelastic mean free path in terms of the electron self-energy:
$$
\lambda \sim \sqrt\frac{E}{2}\frac{1}{|Im(\Sigma(E))|}\;,
$$
where $\Sigma(E)$ is the self-energy, which self-consistently determines the energy of the electron quasi-particle like: $E = \frac{p^2}{2} + \Sigma(E)$. (In units where $e=m=1=\hbar$.)
N.b., The above equation can be understood very roughly in terms of a "wave function" with a complex energy $\Psi \sim e^{-iEt}$. Such a wave function would decay since $|\Psi|^2 \sim e^{-i(\Sigma - \Sigma^*)t} = e^{-2|Im(\Sigma)|t}$. Then the expression for the mean free path follows from defining $v \tau = \lambda$ (as above) and $\tau=\frac{1}{2|Im(\Sigma)|}$ and $v^2\sim 2E$.
Again, the dielectric function is seen to be important because the position-dependent self-energy is known (under certain approximations) to be given by:
$$
\Sigma(\vec r, \vec r'; E) \approx i\int \frac{d\omega}{2\pi}e^{-i\omega\delta}G(\vec r, \vec r'; E-\omega)\int \frac{d^3q'}{(2\pi)^2}e^{i\vec q'\cdot (\vec r - \vec r')}\frac{4\pi}{q^2 \epsilon(\vec q,\omega)}
$$
- How come this curve is similar for all solids, when the environments of the electron must differ quite drastically in different materials?
It's roughly similar because most solids can be roughly characterized as having a dielectric function with a peak near that solid's "plasma frequency," which tends to be in the tens of eVs. Of course, for heavier elements that can be pushed out closer to a hundred eV, but still the dielectric response usually falls off quite fast below the plasma frequency.
The local environment of atoms in a solid can be probed by electronic inelastic scattering or x-ray absorption, but those effects tend to be considered mainly when looking at the oscillations of the spectra near an absorption edge. In other words, a really fast electron, or a high-energy x-ray photon, doesn't "care a lot" about the local structure of the solid. The solid just looks roughly like a soup of atoms with number density $n$ to the fast probe. The number density of solids doesn't change "too much" from solid to solid (and only affects as an overall scale factor). The plasma frequency of various solids does change, but it tends to be in the tens of eV and it tends to characterize the energy scale below which it is hard to make electronic excitations.
One reference textbook that I liked back in the 2000s is linked here. I think it is a reasonably straightforward and readable textbook on inelastic electron scattering. Unfortunately, it seems to only be available in paperback, and seems a bit expensive. But it is the reference I would look at to refresh myself if needed.