What type of bifurcation is this?

Question

Consider the dynamical system

$$ dx/dt = -\cos(r)\sin(x) $$

Clearly $x=0$ and $x=\pi$ are two fixed points of this system. The stability of these two fixed points change as r is varied. Starting from $r=0$, the zero fixed point is initially stable but becomes unstable at $r=\pi/2$ and the opposite happens for the other fixed point.

Is this a transcritical bifurcation? I have so far only seen systems where one of the fixed point approaches the other fixed point and their stability switch as they cross each other.

However in my system, the fixed points remain at the same values of $x$. Only stability changes. If not transcritical, what type of bifurcation is this?

Answer 1

TL;DR: I don't believe the system displays a transcritical bifurcation.

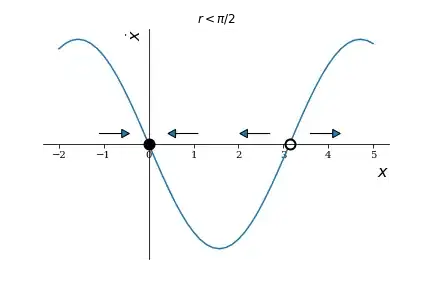
Your stability analysis is correct. For instance, for $r=0$, $\dot{x}$ is simply a negative sine function, so positive $x\approx 0$ values have negative derivatives (and decrease, i.e., move towards zero) and negative values have positive derivatives (so increase and also move towards zero), i.e., $x=x^*=0$ is stable for $r<\pi/2$. See figure below:

And the system does go through a bifurcation as $r$ is varied — though not one of the simple ones, due to the singular nature of the system at $r=r^*=\pi/2$: For this value of $r$ all points $x\in[0,2\pi]$ are (neutrally stable) fixed points, since the system is simply $dx/dt=0$. That's how I'd sketch its bifurcation diagram:

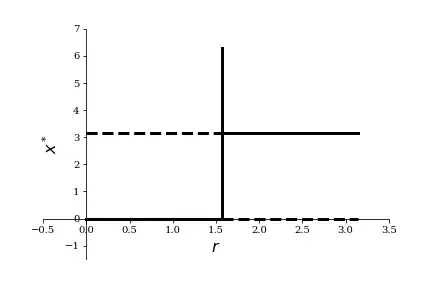
It looks like we could say there's a collision on $r^*=\pi/2$ and the fixed points "exchange stabilities — just like in a transcritical bifurcation, however, I think we have something different here, for two reasons:

I. If we check the formal conditions for the system $\dot{x}=f_r(x)$ to go through a transcritical bifurcation (e.g., Guckenheim & Holmes or Wolfram MathWorld), we'll see they are: \begin{align} f_r(x)\Bigr|_{\forall r, x=x^*}=0 \tag{equilibria}\\ \frac{\partial f_r}{\partial x}\Bigr|_{r=r^*, x=x^*} = 0 \tag{null eigenvalue}\\ \frac{\partial^2 f_r}{\partial r\partial x}\Bigr|_{r=r^*, x=x^*} \ne 0 \tag{TC1}\\ \frac{\partial^2 f_r}{\partial^2 x}\Bigr|_{r=r^*, x=x^*} \ne 0 \tag{TC2} \label{TC2} \end{align} where TC stands for transversality condition. And it's clear that our $f_r(x)$ fails to satisfy \ref{TC2}.

II. By changing variables, $r \mapsto -r + \pi/2$, the system becomes $f_r(x)=-\sin(r)\sin(x)$ and $r^*=0$. If we then try to put $f_r(x)$ in a algebraic normal form, by Taylor expanding it around $(r^*,x^*)$ we obtain, after a new change of variables $r\mapsto r-r^3/6$, $$ f_r(x) = rx -r\frac{x^3}{6} +O(5) $$ which I don't believe can be put in the normal form for the transcritical bifurcation, nor any of the other simple ones: \begin{align} \dot{x} &= r - x^2 \tag{saddle-node}\\ \dot{x} &= rx - x^2 \tag{transcritical}\\ \dot{x} &= r - x^3 \tag{pitchfork} \end{align} Which is perhaps not that surprising, given the system's bifurcation diagram.