Why electric field is scaled by gamma?

Question

Two opposite charges are in a spaceship and are attracted by the electric field $E_s$ But for an observer on earth the Electric force is $$E_e=\gamma E_s$$ Normally the forces are scaled down by $\gamma$ in the earth frame and here also the total force is scaled down. But why the Electric component of force is scaled up? Is it because the Electric fields are now closer together because of length contraction?

But i think this is not the answer because if that was the case,then gravitational fields and hence Forces would have scaled up.But this is not the case in nature. Can you provide a derivation or something which explains how the Electric field is scaled up?

Answer 1

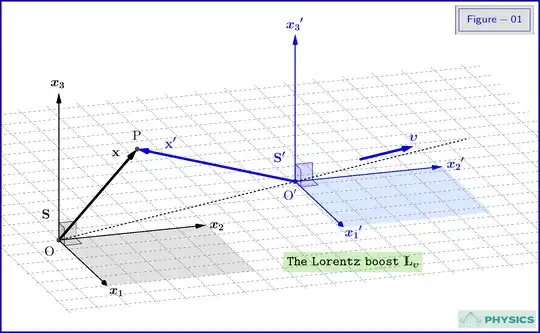
In above Figure-01 an inertial system $\:\mathrm S'\:$ is translated with respect to the inertial system $\:\mathrm S\:$ with constant velocity
\begin{align} \boldsymbol{\upsilon} & \boldsymbol{=}\left(\upsilon_{1},\upsilon_{2},\upsilon_{3}\right) \tag{02a}\label{02a}\\ \upsilon & \boldsymbol{=}\Vert \boldsymbol{\upsilon} \Vert \boldsymbol{=} \sqrt{ \upsilon^2_{1}\boldsymbol{+}\upsilon^2_{2}\boldsymbol{+}\upsilon^2_{3}}\:\in \left(0,c\right) \tag{02b}\label{02b} \end{align}

The Lorentz transformation is \begin{align} \mathbf{x}^{\boldsymbol{\prime}} & \boldsymbol{=} \mathbf{x}\boldsymbol{+} \dfrac{\gamma^2}{c^2 \left(\gamma\boldsymbol{+}1\right)}\left(\boldsymbol{\upsilon}\boldsymbol{\cdot} \mathbf{x}\right)\boldsymbol{\upsilon}\boldsymbol{-}\dfrac{\gamma\boldsymbol{\upsilon}}{c}c\,t \tag{03a}\label{03a}\\ c\,t^{\boldsymbol{\prime}} & \boldsymbol{=} \gamma\left(c\,t\boldsymbol{-} \dfrac{\boldsymbol{\upsilon}\boldsymbol{\cdot} \mathbf{x}}{c}\right) \tag{03b}\label{03b}\\ \gamma & \boldsymbol{=} \left(1\boldsymbol{-}\dfrac{\upsilon^2}{c^2}\right)^{\boldsymbol{-}\frac12} \tag{03c}\label{03c} \end{align}

For the Lorentz transformation \eqref{03a}-\eqref{03b}, the vectors $\:\mathbf{E}\:$ and $\:\mathbf{B}\:$ of the electromagnetic field are transformed as follows \begin{align} \mathbf{E}' & \boldsymbol{=}\gamma \mathbf{E}\boldsymbol{-}\dfrac{\gamma^2}{c^2 \left(\gamma\boldsymbol{+}1\right)}\left(\mathbf{E}\boldsymbol{\cdot} \boldsymbol{\upsilon}\right)\boldsymbol{\upsilon}\,\boldsymbol{+}\,\gamma\left(\boldsymbol{\upsilon}\boldsymbol{\times}\mathbf{B}\right) \tag{04a}\label{04a}\\ \mathbf{B}' & \boldsymbol{=} \gamma \mathbf{B}\boldsymbol{-}\dfrac{\gamma^2}{c^2 \left(\gamma\boldsymbol{+}1\right)}\left(\mathbf{B}\boldsymbol{\cdot} \boldsymbol{\upsilon}\right)\boldsymbol{\upsilon}\boldsymbol{-}\!\dfrac{\gamma}{c^2}\left(\boldsymbol{\upsilon}\boldsymbol{\times}\mathbf{E}\right) \tag{04b}\label{04b} \end{align}

Nothing more, nothing less.

How the Lorentz force 3-vector or the Lorentz force 4-vector are transformed see my answer here Are magnetic fields just modified relativistic electric fields?.

Expressions of the kind $''$...scaled down by $\gamma$...$''$ or $''$...the Electric fields are now closer together because of length contraction...$''$ are misplaced.

Answer 2

Normally the forces are scaled down by γ in the earth frame and here also the total force is scaled down. But why the Electric component of force is scaled up?

The actual derivation is based on Lorentz transformation equations but one intuitive way to visualise this is to visulalise the electric field lines. In a charge at rest, the field lines are pointing outward uniformly in all directions.

But, in a charge that is moving , the field lines get "scrunched up" in the transverse direction to the field of motion, so that the electric field strength in that direction increases

Answer 3

Electric field E transforms this way:

$$E'=\gamma E$$

Gravity field G transforms this way:

$$G'=\gamma G$$

Force F, be it electric or gravitational, transforms this way:

$$ F'= F / \gamma $$