A lot of effort is put into shifting the Fermi energy of a topological insulator to exactly zero which then provides some advantages when this TI is coupled with a superconductor.
I don't understand why this is important or what advantages this should bring. Didn't Kane and Fu in 2008 (see: *) proposed the creation of a Majorana fermion explicitly for a TI that does not have the chemical potential at zero?
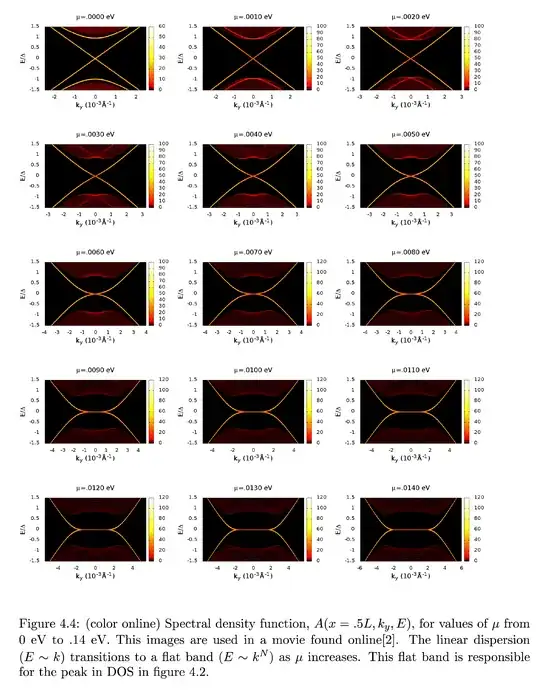
There are many schemes to make topological superconductors. Some of these schemes have restrictions on the chemical potential $\mu$. You also need to know what type of topological superconductors you are dealing with. You can refer to the periodic table to determine this:
In the paper from the link you provided the authors mention two types of superconductors $p+ip$ and the topological insulator + $s$-wave superconductor hybrid; these two represent class D and DIII respectively. For this particular DIII topological superconductor, which the authors discuss in detail in this paper, there does not appear to be any strict restriction on chemical potential being zero. Throughout the paper they set $\mu = 0$ to make the algebra easier. Check the line at the bottom of the first page:
A zero energy solution exists for any $\mu$. The algebra is simplest for $\mu = 0$, where the zero mode has the form ...
The only restriction you have on the chemical potential is that it should lie in the bulk gap. In order to illustrate the reason behind this let me give you an example of a D class topological superconductor. I know this is different from the Fu-Kane proposal but it is more pedagogical. At the end of my example I will draw similarities between the two schemes. The engineering techniques are different but the physics (the end result) is still the same. The $p+ip$ example is from the proposal by:
In this paper they show how you can engineer a 2D spinless $p+ip$ using a sandwich of a conventional superconductor, a 2D electron system with Rashba spin-orbit coupling, and a ferromagnetic insulator (see the figure below).
In the absence of any spin-orbit coupling the dispersion of a 2DEG would simply be $$E(\mathbf{k})=\frac{\hbar^{2}\mathbf{k}^{2}}{2m^{*}}=\frac{\hbar^{2}}{2m^{*}}(k_{x}^{2}+k_{y}^{2})$$ which is nothing but a paraboloid with its center at the origin in $\mathbf{k}$-space. Note that these are actually two degenerate paraboloids one for each spin; in the absence of spin orbit coupling, you have spin degeneracy and hence it’s redundant to consider both of them separately. In the presence of Rashba spin-orbit coupling, however, these paraboloids split into two with their origins at $\pm\mathbf{k}_{0}$ where $\mathbf{k}_{0}$ depends on the direction of the electric field. The band structure of the Rashba spin-orbit coupled system is shown by the gray curves (or surfaces) in the figure below
Now, if we try to reinterpret this band structure in a different basis then we can imagine two bands, the upper and lower portions of the gray surfaces, which touch at the origin. In other words, there is no band gap. This is where the ferromagnetic insulator comes in; it opens a gap at $\mathbf{k} = 0$ and you get two bands (blue surfaces in the above figure). The Zeeman field due to the ferromagnetic insulator has split the bands such that the two bands have different spin projections along the $z$-axis; i.e. upper and lower bands have different eigenvalues for the $S_z$ operator. However, it is important to note that the $x$ and $y$ components of the spins “wind” in $\mathbf{k}$-space as shown in
This is perfect for the conventional superconductor at the top! Due to the proximity effect from the $s$-wave superconductor the electrons at diametrically opposite positions on the paraboloid (with opposite in-plane spin projections) will pair up. But it is important to note, from the third figure, that unless the chemical potential is in the gap (of the blue bands), the system will have two Fermi surfaces (or curves); i.e. it will intersect both bands. You cannot create a topological superconductor if you have two Fermi curves. One naïve way to justify this is an analogy to the two-band model ($H(\mathbf{k})=\vec{d}(\mathbf{k})\cdot\vec{\sigma}$) for topological insulators. If you intersect both bands then the winding (responsible for the non-trivial Berry phase) in one band will cancel the winding of the other; they wind in opposite directions. The only way to have nonzero winding is if you intersect only one band.
Now, there is a fancy name which I carefully omitted from the above discussion: the Nielsen-Ninomiya theorem or Fermion-Doubling Theorem. After all these roundabout tricks, all we wanted was a single spin-polarized Fermi surface. The above theorem effectively boils down to saying that you will typically always have two Fermi surfaces, degenerate or not. We need to work really hard to “bypass” this theorem. The reason behind so much activity in topological superconductivity and emergent Majorana fermions after the discovery of topological insulators is that a violation of the fermion-doubling theorem comes for free! There is some subtlety to it. This theorem is not wrong; it is possible to reconcile it with topological insulators. You can read about this elsewhere. But what’s really important is this: if the chemical potential of a 3D topological insulator is placed in the bulk gap (not necessarily the Dirac point on the surface) then you get a non-degenerate spin-polarized Fermi curve on one of faces the surface. Then, once you bring in the other ingredients: gapping the spectrum and inducing pairing, you will end up with a topological superconductor.
I actually answer this exact question in this paper (http://arxiv.org/abs/1207.5534 http://prb.aps.org/abstract/PRB/v86/i16/e161108). Yes, it's shameless self-publicity, but what can you do.
The story in a nut shell is as simply the linear Majorana dispersion ($E\propto k$) morphs into a quadratic dispersion ($E\propto k^2$) then into a flat dispersion ($E\propto k^N$) as $\mu$ increases away from the Dirac point. See images below
