Click here for reference. Then as far as tidal potential energy goes in terms of displacements...
$$\frac{\Delta {{r}_{sun}}}{\Delta {{r}_{moon}}}\simeq \frac{{{m}_{sun}}}{{{m}_{moon}}}\frac{{{R}_{moon}}^{3}}{{{R}_{sun}}^{3}}\simeq \frac{1.99\times {{10}^{30}}}{7.35\times {{10}^{22}}}\frac{{{\left( 3.84\times {{10}^{8}} \right)}^{3}}}{{{\left( 1.5\times {{10}^{11}} \right)}^{3}}}\simeq 4.29\times {{10}^{30-22+24-33}}\\\simeq 4.29\times {{10}^{-1}}\simeq 43\%$$
UPDATE: (based on comments)
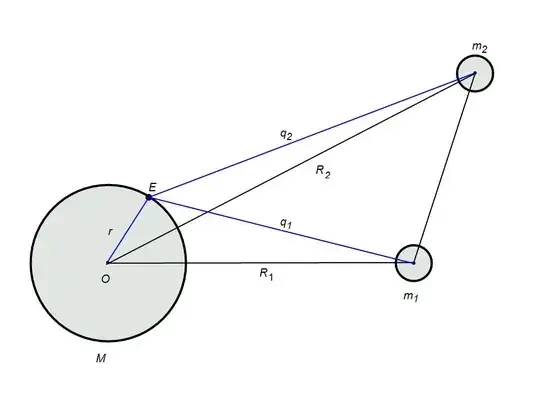 Consider two masses ${{m}_{1}}$ and ${{m}_{2}}$ whose co-ordinates are measured relative to the centre of a third mass, M, via distances ${{r}_{1}}$ and ${{r}_{2}}$. Point E lies on the surface of mass M (assumed to be spherical) and for now is assumed to also be in the plane of all three masses for convenience. Let $\angle EO{{R}_{1}}=\theta $and $\angle {{R}_{2}}O{{R}_{1}}=\phi $. We have using the same approximations as before
$${{V}_{T}}={{V}_{m1}}+{{V}_{m2}}=-\frac{G{{m}_{1}}{{r}^{2}}}{2R_{1}^{3}}\left( 3\cos \left( \theta \right)-1 \right)-\frac{G{{m}_{2}}{{r}^{2}}}{2R_{2}^{3}}\left( 3\cos \left( \theta -\phi \right)-1 \right),0\le \phi ,\theta \le \frac{\pi }{2}$$
Tidal displacement due to both moon, ${{m}_{1}}$and sun, ${{m}_{2}}$ as a first approximation can be given by
$$\Delta r=\frac{{{r}^{4}}}{2M}\left\{ \frac{{{m}_{1}}}{R_{1}^{3}}\left( 3\cos \left( \theta \right)-1 \right)+\frac{{{m}_{2}}}{R_{2}^{3}}\left( 3\cos \left( \theta -\phi \right)-1 \right) \right\}$$
From which we have then
$$\Delta {{r}_{spring}}=\frac{{{r}^{4}}}{2M}\left\{ \frac{{{m}_{1}}}{R_{1}^{3}}+\frac{{{m}_{2}}}{R_{2}^{3}} \right\}\left( 3\cos \left( \theta \right)-1 \right)$$
and
$$\Delta {{r}_{neap}}=\frac{{{r}^{4}}}{2M}\left\{ \frac{{{m}_{1}}}{R_{1}^{3}}\left( 3\cos \left( \theta \right)-1 \right)+\frac{{{m}_{2}}}{R_{2}^{3}}\left( 3\sin \left( \theta \right)-1 \right) \right\}$$
Q: Are there positions on the earth where the tidal displacement for both a spring and neap tide are the same? Equating the two displacements we find $\cos \left( \theta \right)=\sin \left( \theta \right)\Rightarrow \theta =\frac{\pi }{4}$ independent of mass. More generally we might ask when the system is not in a neap-tide, then where will the displacements become equal to that when it is in a neap-tide. Then we are considering
$$\sin \left( \theta \right)=\cos \left( \theta -\phi \right)=\sin \left( \tfrac{1}{2}\pi -\theta +\phi \right)\Rightarrow \theta =\tfrac{1}{4}\pi +\tfrac{1}{2}\phi $$
Which defines a function $\theta \left( \phi \right)$ describing a point on the earth which has a displacement equivalent to that at neap tide. Note: $\theta \left( 0 \right)=\arctan \left( 1 \right)=\frac{\pi }{4}$ which was our previous result. So the point moves linearly with respect to angular separation, starting at $\pi /4$ in a spring tide and converging upon itself at a neap tide (which we logically expect). Note that this analysis delivers a single point where rather I think it would be a locus of points created at the intersection of two spheroids. We have the prolate spheroidal bulge due to the moon, which we hold fixed, and then add to that a tilted spheroid from the sun which as it moves towards its position for a neap-tide, becomes an oblate-spheroid. As it tilts it creates a locus of intersections on the surface where tidal displacements are equivalent to that at a neap-tide. Also there are other solutions here i haven't considered (due to the periodicity of the functions) in which a more careful analysis will bring to the fore. However i'd suggest moving directly to a more general coordinate set and try and capture the full locus.
Consider two masses ${{m}_{1}}$ and ${{m}_{2}}$ whose co-ordinates are measured relative to the centre of a third mass, M, via distances ${{r}_{1}}$ and ${{r}_{2}}$. Point E lies on the surface of mass M (assumed to be spherical) and for now is assumed to also be in the plane of all three masses for convenience. Let $\angle EO{{R}_{1}}=\theta $and $\angle {{R}_{2}}O{{R}_{1}}=\phi $. We have using the same approximations as before
$${{V}_{T}}={{V}_{m1}}+{{V}_{m2}}=-\frac{G{{m}_{1}}{{r}^{2}}}{2R_{1}^{3}}\left( 3\cos \left( \theta \right)-1 \right)-\frac{G{{m}_{2}}{{r}^{2}}}{2R_{2}^{3}}\left( 3\cos \left( \theta -\phi \right)-1 \right),0\le \phi ,\theta \le \frac{\pi }{2}$$
Tidal displacement due to both moon, ${{m}_{1}}$and sun, ${{m}_{2}}$ as a first approximation can be given by
$$\Delta r=\frac{{{r}^{4}}}{2M}\left\{ \frac{{{m}_{1}}}{R_{1}^{3}}\left( 3\cos \left( \theta \right)-1 \right)+\frac{{{m}_{2}}}{R_{2}^{3}}\left( 3\cos \left( \theta -\phi \right)-1 \right) \right\}$$
From which we have then
$$\Delta {{r}_{spring}}=\frac{{{r}^{4}}}{2M}\left\{ \frac{{{m}_{1}}}{R_{1}^{3}}+\frac{{{m}_{2}}}{R_{2}^{3}} \right\}\left( 3\cos \left( \theta \right)-1 \right)$$
and
$$\Delta {{r}_{neap}}=\frac{{{r}^{4}}}{2M}\left\{ \frac{{{m}_{1}}}{R_{1}^{3}}\left( 3\cos \left( \theta \right)-1 \right)+\frac{{{m}_{2}}}{R_{2}^{3}}\left( 3\sin \left( \theta \right)-1 \right) \right\}$$
Q: Are there positions on the earth where the tidal displacement for both a spring and neap tide are the same? Equating the two displacements we find $\cos \left( \theta \right)=\sin \left( \theta \right)\Rightarrow \theta =\frac{\pi }{4}$ independent of mass. More generally we might ask when the system is not in a neap-tide, then where will the displacements become equal to that when it is in a neap-tide. Then we are considering
$$\sin \left( \theta \right)=\cos \left( \theta -\phi \right)=\sin \left( \tfrac{1}{2}\pi -\theta +\phi \right)\Rightarrow \theta =\tfrac{1}{4}\pi +\tfrac{1}{2}\phi $$
Which defines a function $\theta \left( \phi \right)$ describing a point on the earth which has a displacement equivalent to that at neap tide. Note: $\theta \left( 0 \right)=\arctan \left( 1 \right)=\frac{\pi }{4}$ which was our previous result. So the point moves linearly with respect to angular separation, starting at $\pi /4$ in a spring tide and converging upon itself at a neap tide (which we logically expect). Note that this analysis delivers a single point where rather I think it would be a locus of points created at the intersection of two spheroids. We have the prolate spheroidal bulge due to the moon, which we hold fixed, and then add to that a tilted spheroid from the sun which as it moves towards its position for a neap-tide, becomes an oblate-spheroid. As it tilts it creates a locus of intersections on the surface where tidal displacements are equivalent to that at a neap-tide. Also there are other solutions here i haven't considered (due to the periodicity of the functions) in which a more careful analysis will bring to the fore. However i'd suggest moving directly to a more general coordinate set and try and capture the full locus.
