Analogy for Lentz soliton

Question

Analogy for Alcubeirre Warp Drive:

Every explanation of warp drive in layman terms has this sentence in it:

"The Warp Drive will contract space in thier front and expand space behind."

(I am not sure that this is literally what the alcubierre metric describes)

And then show pictures like this:

They also use the analogy of a surf board surfing in the sea.

This analogy of surf board makes it intuitive to understand how warp drives work.

Analogy for Lentz Soliton:

Recently I have been hearing that Eric Lentz published a paper concluding that we can have warp drive without the need of negative energy to expand spacetime.

When I search lentz soliton on google, it shows this picture:

It is absolutely not intuitive how the the lentz soliton works.

In the case of alcubeirre warp drive, it was intuitive that space pushes the drive from behind and pulls from the front.

Question:

I want an intuitive analogy about how the Lentz Soliton works, if there are any.

Answer 1

Basically, he came up with a way to generate both the push and the pull force without needing to create negative energy, which as far as we know is impossible to do. Since energy and mass are interchangeable due to the well known equation E=mc^2, and mass can warp space time (aka it creates gravity) that in turn means that energy can also warp space time. What warp drive designs do, is contract the space time in front of them, aka they create a gravitational attraction in front of them, and expand the space time behind them, aka ANTI gravity, which since there is no negative mass and there is no way to create any significant amount of negative energy, is impossible. Lentz warp drive design is arranged in such a way that the ship is propelled forwards without needing the negative energy or reverse gravity behind it. Not all scientists are convinced of his designs validity, but he maintains his belief in it’s authenticity.

Answer 2

The explanation about expanding and contracting space is unfortunately an incorrect explanation of how warp drives move. Rather, it is an artefact from the times when the Alcubierre metric was proposed.

When Miguel Alcubierre's paper came out in 1994, it appeared that Alcubierre solution needed something special to move, and coincidentally Alcubierre metric has an expanded and contracted regions behind and in front of the bubble (Alcubierre paper: https://arxiv.org/abs/gr-qc/0009013, https://iopscience.iop.org/article/10.1088/0264-9381/11/5/001). So, the explanation quickly made it to the popular domain.

In 2002, Jose Natario had constructed a class of warp drives which could travel like the Alcubierre drive, but did not have any contracted or expanded regions around the bubble (Natario paper: https://arxiv.org/abs/gr-qc/0110086, https://iopscience.iop.org/article/10.1088/0264-9381/19/6/308). In other words, Natario showed that expansion and contraction have nothing to do with the motion of the warp bubble. Unfortunately, the correct explanation did not make it into the popular domain.

Erik Lentz's solution (Lentz paper: https://arxiv.org/abs/2006.07125, https://iopscience.iop.org/article/10.1088/1361-6382/abe692), just like the warp drives in the Natario class, does not need expansion and contraction to move.

In fact, the recent Bobrick paper (Bobrick paper: https://arxiv.org/abs/2102.06824, https://iopscience.iop.org/article/10.1088/1361-6382/abdf6e) shows that all physical drives move inertially, and can only accelerate by propulsion.

In summary, warp drives move because they already move, or else they need to propel, and their movement is not related to spacetime expansion or contraction.

Answer 3

Very good point, it goes to the heart of the debate around warp drive: what is the physical process that causes the warp drive bubble to move? And what would cause it to reach FTL speed? As I see it, there are two positions/hypotheses:

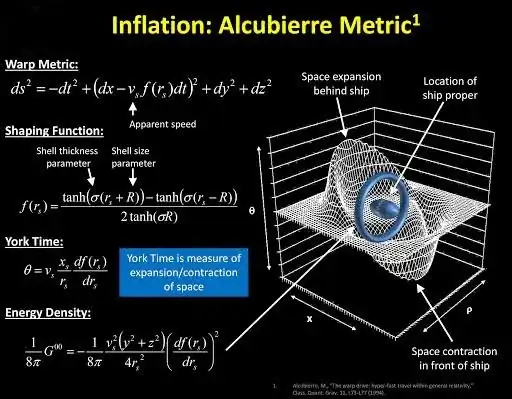
A): The original Alcubierre one, which says that the expansion/contraction of spacetime is the causal effect. The direction of travel is that space contracts in front of the bubble, expands behind it. In effect, the mechanism that causes the expansion of the Universe is "at work" locally and in a narrowly directed line. Just as the c-barrier does not apply to the expansion of the Universe, it does not apply to this. There is no detailed, computational model of how the bubble would reach FTL velocity. But this conception doesn't require it to be done by some kind of conventional spacecraft propulsion, but somehow it is done by expansion/contraction. (Alcubierre paper: https://arxiv.org/abs/gr-qc/0009013), (Alcubierre, Lobo paper https://arxiv.org/abs/2103.05610), (Lobo, Visser paper: https://arxiv.org/abs/gr-qc/0406083)

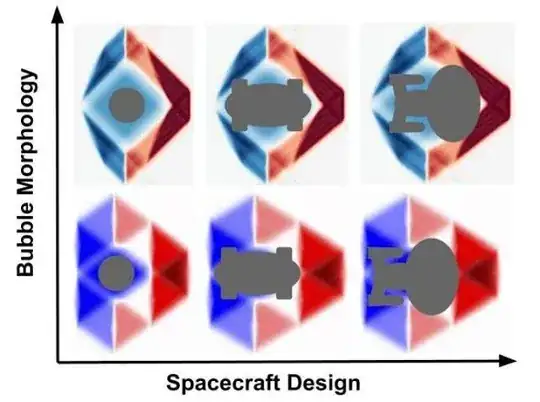
B) The other one that has become more common in recent years is that it is not the expansion/contraction of space-time that causes the warp drive to proceed, it is only incidentally related to it in some models. There are warp drive spacetimes with no expansion and contraction. According to this there is no realistic physical process behind it all, so the expansion of the universe is not a good analogy either. So warp drive is, for now, just a kind of paper-defined way of moving that fits with the rules of general relativity. Some unknown and as yet unimaginable drive would have to provide the FTL speed for the bubble. According to this, the position of a warp drive would in fact be the same as, not more realistic than the imaginary tachyons. (Bobrick,Martire paper: https://arxiv.org/abs/2102.06824)

As far as we know, neither hypothesis A) nor B) have been proven or disproven, but are competing alternatives. Important question raised here: if a new warp drive model is discovered, like Lentz, which version does it fit? Can we place it among those in which expansion and contraction can be detected and thus support that such a realistic effect can generate FTL motion? Or, on the contrary, is it rather a counter-example?

But the proponents of version B) not only claim to have developed a new hypothesis, they also claim that version A) is a fallacy which they have disproved and version B) has been proven. This is the sense of the Bobrick-Martire study and the main answer here, with which the questioner agreed, strongly states.

But it is not clear where this follows from, where would it be proven to be so? The Alcubierre-warp drive articles definitely attribute it to the effect of expansion/contraction, also for equivalent spacetimes (van den Broeck spacetime etc.) The main claim of Bobrick's answer here is, "warp drives move because they already move, or else they need to propel, and their movement is not related to spacetime expansion or contraction." I see he refers to the Natario article as having already demonstrated this.

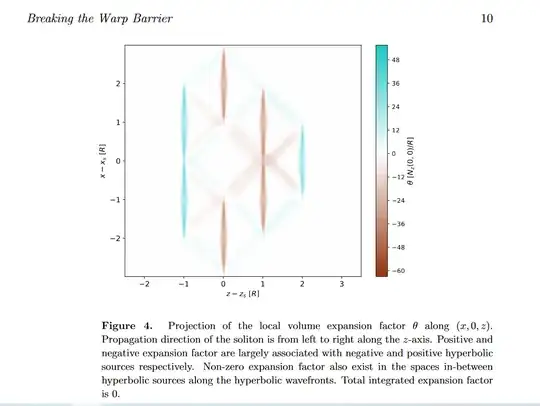
But in the Natario warp drive there is also expansion and contraction, just not in front of and behind the bubble, but trickier. This is clarified on page 5 of the article by Natario: "This gives some insight into the geometry of this spacetime: for example for cos θ > 0 (i.e., in front of the bubble), Krr < 0 where f ′ > 0 (i.e., in the bubble's wall), indicating a compression in the radial direction; this is however exactly balanced by Kθθ + Kϕϕ = -Krr, corresponding to an expansion in the perpendicular direction". Although the title of the article is indeed "WARP DRIVE WITH ZERO EXPANSION", and in the introduction the author also says that "this contraction/expansion is not necessary at all, and that in particular it is possible to construct a similar spacetime where no contraction/expansion occurs.". But as far as I can see, in his solution this does not mean that there is no expansion or contraction at all. It means that there is a different type than in the Alcubierre type and that, overall, contraction and expansion compensate each other. Thus, the essential property of the warp drive is revealed to be the change in distances along the direction of motion, and not the expansion/contraction of space volume. (Natario paper: https://arxiv.org/abs/gr-qc/0110086) Thus, in my opinion, the paper is contradictory and does not prove that warp drive motion has nothing to do with the expansion/contraction of spacetime. Is there an example in the Bobrick-Martire study of a warp drive spacetime that has no expansion or contraction? Also, is there any proof more generally that version A) is incorrect?

Furthermore, suppose that they produce on paper a warp drive spacetime that really has no space contraction/expansion. This is an interesting theoretical development. But why would it prove that for warp drive models that do have expansion and contraction, it is not the cause of motion? The fact that we can theoretically design different models does not negate the properties of the original model.

The other main, related issue is acceleration and propulsion. B) says that this has nothing to do with the expansion/contraction of spacetime either, it would not cause the warp drive to progress. Rather it would require some kind of conventional and unknown propulsion that would accelerate the bubble to FTL speed. It is not clear what evidence there is to support this. The Bobrick-Martire paper discusses the issue in chapter 5, and what I see there seems more opinion than proof. They categorizes as an error that Alcubierre originally introduced a time-dependent velocity into the metric, so his construction violates energy conservation. Am I right in thinking that Noether's theorem is behind this? That is, if we have a spacetime whose metric and hence Lagrange function is explicitly time dependent, then there is no energy conservation theorem for it. The best known example of this in standard cosmology is the spacetime describing the Universe, the Robertson-Walker metric. Yes, there is no binding energy conservation for the entire Universe - and that's not a problem. But I don't see why, in the case of the Alcubierre metric, a similar explicit time dependence would be a problem that should be corrected, that should be got rid of.

Answer 4

I will now try to answer the question posed in concrete terms. In my previous answer, I wrote about the general questions and problems of warp drive research, which are important and necessary in themselves in order to analyse the properties of the Lentz soliton. So an important and interesting question is: how can we place the newly published warp drive model Lentz-soliton in the known warp drive field? Is it similar to those in which expansion and contraction can be detected behind and in front of the bubble? (as in the Alcubierre type). Does this support the idea that such a realistic effect generates superluminal motion? Or, on the contrary, is it more of a counter-example and an argument for those who believe that spacetime expansion and contraction have nothing to do with warp drive in any meaningful way?

Let's look at the relevant figure from Lentz's article:

The Lentz soliton runs from left to right, along the z axis. This projection has an interesting, angular hexagonal shape. The quantity θ, which measures the expansion of the local volume, is shown. (It's another name is York time).It is the same as the well-known driving wave in the Alcubierre type, deeply negative in front of the bubble and strongly positive behind it. Here the blue colour is now the positive range, the brown is the negative range. What do we see? At the back of the bubble, at -1, there are two strong converging expansion bands. In the middle, at 0, there are two separated contraction bands. Then, towards the front, at 1, strong connected contraction bands; finally, at the very front, at 2, expansion, but half as much as at the back.

This is essentially similar to the Alcubierre type. Expansion at the back, contraction at the middle and front. A similar intuitive picture can be drawn as for that one. So it contracts at the front, expands at the back, and that's what drives it forward. The only range that doesn't fit the picture is the expansion at 2 - but it's reasonable to think that this weakens the effect, but doesn't "overcome" all the contraction at the front.

Thus, judging from the original article, the Lentz soliton in this respect falls into the Alcubierre type and does not support the Bobrick-Martire study's assessment that the warp drive has nothing to do with the expansion and contraction of spacetime. In terms of the energy required, of course, the Lentz warp drive is very different from the Alcubierre type (and from all the others so far). Since it does not require exotic matter, the energy density in the whole range is such that it satisfies the energy conditions, i.e. positive. Therein lies its pioneering significance. (Lentz paper: https://arxiv.org/abs/2006.07125)