My question is about the input output formalism. In the original paper, the authors, Gardiner & Collet, describe the interaction of a system with a continuum of modes via the Hamiltonian:
$$H=H_S+\int_{0}^{+\infty} d \omega \ \hbar \omega b^{\dagger}_{\omega} b_{\omega}+i \int_0^{+\infty} d \omega \ \hbar g(\omega) (b^{\dagger}(\omega) c - b(\omega) c^{\dagger})$$
Where the operators $c$ and $c^{\dagger}$ are annihilation/creation operators acting on the system S, the operators $b(\omega)$ satisfy the commutation relations:
$$[b(\omega),b^{\dagger}(\omega')]=\delta(\omega-\omega')$$ $$[b(\omega),b(\omega')]=0$$
In the paper, they say that they extend to $-\infty$ the integrals to make calculations easier (explained in the paragraphs right after 2.2).
My question is: how to properly get to this kind of Hamiltonian in a particular setup: qubit put at the end of a semi infinite waveguide.
The physical model I consider
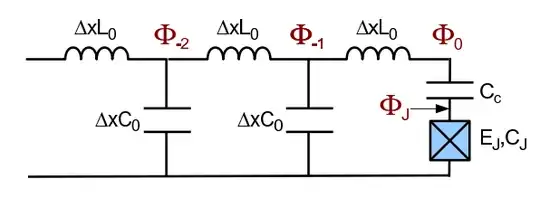
I am following this paper. Basically a superconducting qubit is capacitively coupled to a waveguide as shown on this picture:
In the end, the Hamiltonian can be written as:
$$H=H_S+H_W+H_{int}$$
With the system Hamiltonian (I call $C_{\Sigma}=C_c+C_J$ and $\phi_0=\hbar/2e$)
$$H_S=\frac{p_J^2}{2 C_{\Sigma}}-E_J \cos(\Phi_J/\phi_0)$$ $$H_W=\frac{C^2_c}{2 C_{\sigma}} (\partial_t \phi(0,t))^2+\int_{-\infty}^{0} \frac{p(x,t)^2}{2C_0}+\frac{\partial_x \Phi(x,t)}{2 L_0}$$ $$H_{int}=\frac{C_c}{C_{\Sigma}} p_J \partial_t \Phi(0,t)$$
To simplify the discussion, we can assume that the system is approximatively an Harmonic oscillator, thus:
$$H_S \approx \frac{p_J^2}{2 C_{\Sigma}}+\frac{E_J}{\phi_0^2}\frac{\Phi_J^2}{2} =\frac{p_J^2}{2m}+\frac{1}{2}m \omega^2 \Phi_J^2$$
With $m=C_{\Sigma}$, and $\omega=\sqrt{E_J/C_{\Sigma}}*1/\phi_0$
The field $\Phi(x,t)$ and its conjugated momentum field: $p(x,t)$ verify for $x<0$ the equation of propagation of a Free field. It gives us:
$$\Phi(x,t)_{\leftrightarrows}=\sqrt{\frac{\hbar Z_0}{4 \pi}}\int_0^{+\infty} \frac{d \omega}{\sqrt{\omega}} a^{\leftrightarrows}(\omega) e^{-i\omega(t \mp x/c)}+h.c$$ $$p(x,t)_{\leftrightarrows}=-i\sqrt{\frac{\hbar Z_0}{4 \pi}}\int_0^{+\infty} d \omega \sqrt{\omega} a^{\leftrightarrows}(\omega) e^{-i\omega(t \mp x/c)}+h.c$$
With $Z_0$ the impedance of the ligne: $Z_0=\sqrt{\frac{L_0}{C_0}}$, and $c=\frac{1}{\sqrt{L_0 C_0}}$ the velocity of waves in this line.
In term of physics, $\dot{\Phi}$ represent the voltage on the associated point, while $p(x,t)$ is the charge density.
First question:
To get an Hamiltonian like the one I wrote, I would simply replace the expression of the free field $\Phi(0,t)$, and express $p_J$ in function of the annihilation/creation operators which would in principle give me an expression that looks like my interacting Hamiltonian $i \int_0^{+\infty} d \omega \ \hbar g(\omega) (b^{\dagger}(\omega) c - b(\omega) c^{\dagger})$ (after neglecting counter rotating terms). I skip the details.
However, I would have in this Hamiltonian two modes $a^{\leftarrow}(\omega)$ and $a^{\rightarrow}(\omega)$.
This might not be a problem in principle but what confuses me is the following.
If I imagine putting an atom not at $x=0$ but somewhat before, at $x=-x_0$ the boundary condition in $x=0$ would give me a relationship between $a^{\rightarrow}(\omega)$ and $a^{\leftarrow}(\omega)$ such that I would only have "half the modes" I am writing here. This is the situation I am more familiar with.
Here the boundary condition is given by some relationship between $a^{\leftarrow}(\omega)$,$a^{\rightarrow}(\omega)$ and the system operators which I don't really know how to interpret in order to get the "half of the modes" result.
The question is thus: how to cleanly write down an Hamiltonian for this system that is suited for the input/output formalism from Gardiner.
Second question
In the paper they proceed to solve the dynamic by calling:
$$\Phi_{in}(t)=\Phi_{\rightarrow}(0,t)$$ and they get some input/output relations. However the input-output formalism which I gave the ref is not simply taking the right moving waves and calling it the input field. It consists in taking the right moving waves and make them freely evolve, thus without the interaction. In their definition of input/output fields, their operators $a^{\rightarrow}(\omega)$ in $\Phi_{\rightarrow}(0,t)$ will not freely evolve because of the interaction with the qubit. For me what they call input and output is not the same as what is done with Gardiner method.
It is not necessarily a problem but I would be interested to confirm if indeed the notion of input/output field they use here is different from the one from Gardiner.
And if it is the case, how to make the connection between the different input-output relations: one I would obtain from Gardiner, and the one they obtain here.