Speed of gravity effect on a circle of stars

Question

I was wondering how the finite speed of gravity waves influences the behaviour of galaxies, and came up with this thought experiment, that seems to give different results when looked at from different reference frames. Forgive me for using Newtonian terminology in the description.

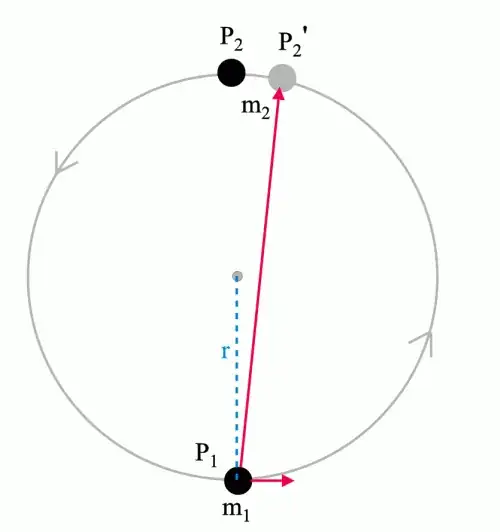
Assume a circle of stars, all of equal mass, distributed equidistantly along the circle. We assume there is no mass in the centre for the moment. Assume the stars all have exactly the correct velocity to travel counterclockwise along the circle. See the 8 black dots representing the stars in this figure:

As seen from the outside inertial frame, the stars are all orbiting around the common centre of mass, they experience a gravitational pull towards the centre of mass, and as a result, only experience acceleration directed towards the centre. Because the situation is fully symmetric, that centre of mass will not move, and the stars keep orbiting forever.

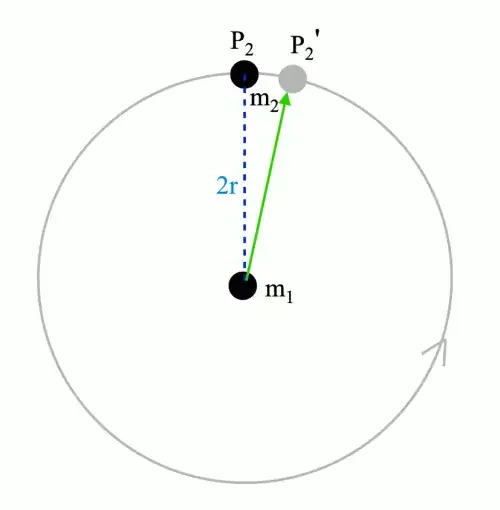
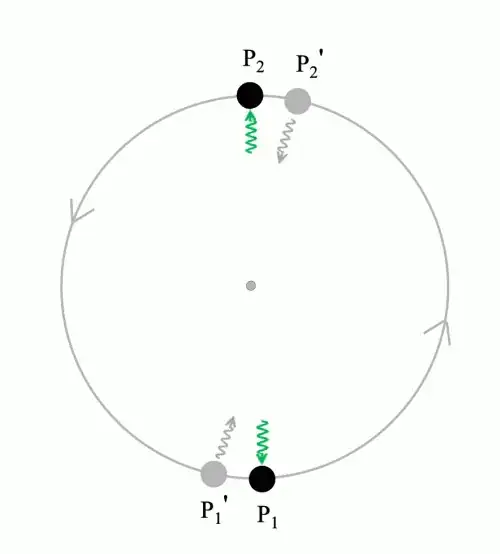
But if we view the situation from one of the stars (the bottom star in the figure above), the situation is different. The gravity from the other stars takes time to reach the star, so their gravitational pull should come from slightly behind their real positions. We assume that gravity travels with the speed of light, then it will appear to pull from a star’s visible location, the white dots in the figure above. As a result, the combined gravity from the other stars shouldn’t pull towards the centre of the circle, but slightly to the right, along the red arrow in the figure.

This should also imply that the star experiences, besides the radial acceleration, also acceleration tangent to the circle. That is, its speed along the circle should increase. Because this situation is fully symmetrical for all stars, all the stars should gain more and more speed over time, and eventually they should spiral away from each other.

Because this can obviously not be true, there must be a mistake in my way of thinking. What is it?

And how does the situation change if there is a black hole in the middle of the circle? Due to the stretching of space around a black hole, gravity should take even longer to reach the other side of the circle?

---

UPDATE: The answer to a similar question quoted by @benrg in the comments, links to the following explanation on the web: https://math.ucr.edu/home/baez/physics/Relativity/GR/grav_speed.html

The main explanation in this essay is:

In that case, one finds that the "force" in GR is not quite central—it does not point directly towards the source of the gravitational field—and that it depends on velocity as well as position. The net result is that the effect of propagation delay is almost exactly cancelled, and general relativity very nearly reproduces the newtonian result.

They also state that the same is true for electro-magnetism:

If a charged particle is moving at a constant velocity, it exerts a force that points toward its present position, not its retarded position, even though electromagnetic interactions certainly move at the speed of light. [...] a calculation shows that the force on A points not towards B's retarded position, but towards B's "linearly extrapolated" retarded position. [...] This is exactly what one finds when one solves the equations of motion in general relativity.

So, in short, the gravity will not appear to come from the actual retarded position, but from an "extrapolated" position.

Is it possible to explain that phenomenon from an intuitive physics point of view, avoiding faster-than-light communication and without going into tensor calculus?

Answer 1

Your argument is inconsistent because the concept of the center of mass, as used by you, implies instantaneous interaction. If you want to use it with retarded interaction, then the center of mass has to refer to the retarded position of the star at the top, not the instantaneous one (after all, that's what the stars interact with). So you have to move the star positions of the 'source'-stars anti-clockwise so that the white dot at the top is opposite to the center of mass and the (irrelevant) black dot left of it.

However, there is a further inconsistency in your picture above: the retarded positions (white dots) as drawn by you refer to the black dot at the bottom, but in the inertial reference frame (fixed in the 'paper' plane), whereas they should refer to the moving star as the latter is the target of the gravity signal here. But for your example all the stars move with the same speed on the circle, so the distance between any two of them never changes. So effectively, all stars are at rest relatively to each other and retardation has therefore no visible effect.

===============================

EDIT (detailing my answer in view of some of the other answers and comments)

If we restrict ourselves to just 2 masses orbiting each other, the argument by the OP (which goes actually back to Laplace more than 200 years ago) can be represented by the following diagram

According to this, mass $m_1$ is accelerated along its orbit as the force to the retarded position of mass $m_2$ is not radial anymore. Hence the orbit would be unstable. But this picture is incorrect. As mentioned already, it would apply to a stationary mass $m_1$ but not an orbiting one. As is obvious, the distance of mass $m_1$ to the retarded position $P_2'$ would be different here from that to the instantaneous position $P_2$. But for two masses in a circular orbit the distance between them must always be the same as $m_1$ moves the same distance within a given time as $m_2$. If we display the orbit of $m_2$ with regard to $m_1$ we get in fact the following picture

Obviously, the retarded position of $m_2$ has the same distance from $m_1$ as the actual position. The situation is thus equivalent to one with instantaneous gravitational interaction and thus there is no effect on the dynamics of the orbit.

The gravitational interaction is something that happens between two masses. It would be incorrect to assume one mass sends out some 'gravitons' that then may (or may not) be absorbed by some other mass. If one wants to display the situation symmetrically in the center of mass reference frame, one should therefore use rather a picture like this

The 'gravitons' are sent out by both masses when at the retarded positions and received when at the instantaneous positions. Assuming that the gravitons obey the invariance principle for the speed of light, the latter does not depend on the relative motion of the masses, so the gravitons are sent and received perfectly radially and thus no retardation effect occurs.

Effects would only occur for elliptical orbits, as there the distance between the masses is variable. For anyone interested, I have recently written a paper which calculates the effect of retardation on the orbits of all the planets; as it turns out, the only effect is a small (retrograde) precession of the orbits (note that this paper is as yet not accepted for publication in a journal, so use it at your own risk).

Contrary to what is frequently claimed, there is thus no General Relativity needed to answer the OP's question, as the retarded force is a central force anyway in a circular orbit.

Answer 2

I think that a simpler example is two objects rotating in a circle, like the top and bottom stars in your diagram. This should be an allowable motion, but if we use a delayed gravity approach the motion cannot be maintained. That's why simply introducing a retarded gravity is not a solution to Newton's instantaneous action at a distance.

Answer 3

There's no contradiction here. You would observe a tangential acceleration, which would mean that the radius of the circle would increase, and the configuration would fly apart. If nothing else, using the retarded time makes the particles slightly farther apart than they would be using instantaneous time, which would make the gravitational force slightly less than what is needed to maintain circular motion.

All you've found is that this is an unstable configuration if you use the retarded time.

Answer 4

You treated the problem as if spacetime is Newtonian (non-curved). In reality, spacetime isn't Newtonian. If you approach the problem in a general relativistic way, you'll find that the orbits will be perfectly circular. The general relativistic calculation is complicated but you can intuitively state that the extra speed gained by the retardation (in the Newtonian spacetime) is canceled by the curvature of spacetime.
As you already stated in your comments, the only way for the stars to see the other stars exactly in the middle and let the gravity come from the middle too (so all the separate CM's will fall together) is to make the photons and the changing gravity field (which can be described by photons, but this is not necessary) curve in the curved spacetime between the stars. This has to be the case because we know that two stars will always stay in a circular orbit (if no gravitational waves are emitted, which isn't so, but that's another story). So somehow, spacetime is curved in such a way that photons and gravitons seem to have their origin in the center of the stars. Quite remarkable! But general relativity shows that it is so.

Answer 5

Feynan describes a similar situation for the electrostatic charge in his Lectures on Physics II-21. After studying his mathematics in detail, I think I have a better understanding now how this works. The key is to realise that the other mass has a geometric size. I’ll try to describe our rotating stars situation, concentrating on how the gravitational field of the opposite star is shaped.

The gravitational potential of a mass

Imagine a single stationary mass (like a star), and consider its gravitational potential. I like to imagine that as a steel ball making an indentation on a rubber sheet, although real connoisseurs of General Relativity will likely cringe at that analogy:

The gravitational potential is the same at the same distance from a stationary mass. If we place another mass anywhere on that, then it is the gradient (the slope of the rubber sheet) of the potential at that point which determines the direction of the acceleration it will obtain. For a stationary mass, that direction is always towards the centre of mass.

Now consider a moving mass instead, as viewed from a stationary point in its path in front of it. The gravitational potential at that point will decrease until the mass passes and will then increase again. In Newtonian physics, with infinite gravity speed, the gravitational potential at that point will always be identical to the stationary potential at the instantaneous distance. In Relativistic physics, where gravity travels at limited speed, you might expect (I did) that the gravitational potential is the same as the stationary potential, but centered on its retarded position. With the retarded position, we mean the position its centre-of-mass had when the gravity left it.

The effect of the geometric size of the mass

But the mass has a geometric size, and the front of the mass is closer to our stationary point than the back of the mass. Because the gravitational potential changes travel with finite speed, the change caused by the front (which lowers the potential), reaches the point before the change caused by the back (which raises the potential). As a result of that difference, the potential in front of the mass is lower than the stationary potential of the retarded position.

For the same reasons, for a stationary point behind the traveling mass, the potential is higher than the stationary potential would be. With the higher potential behind the mass, and the lower potential in front of the mass, there is effectively an extra gradient in the direction of travel of the mass.

Now, in our rotating stars situation, when we view a moving star from an opposite star, we are not at a point in front of or behind the retarded position, but at a point to the side. In that case, the gravitational potential itself is the same as the stationary potential of the retarded position. But the extra gradient is still there as well. The stationary gradient is directly towards the retarded position, but the extra gradient turns that direction more towards the direction of travel of the other mass. The combined gradient causes acceleration towards the projected retarded position. That is, towards the instantaneous position that the mass will have assuming it continues to travel with the same speed and direction. With low accelerations, that position is approximately identical to the real instantaneous position.

The resulting gravitational potential

If we take a snap-shot (at a stationary time) of the gravitational potential of the traveling star, then we get a picture similar to the following:

The star is traveling along the red line, with its retarded position at 0, and its instantaneous position at point 3. Imagine the other star is located at the green -6 mark. Note the (small) gradient at that point towards the positive red direction.

---

PS 1: Note that the gravitational field is compressed in the direction of travel; it is shorter in the red direction than in the green direction. This is due to the Lorentzian length contraction.

PS 2: in the above I stressed that the extra gradient is due to the geometric size of the mass. Although that is true, Feynman shows that, if the size is small enough, that the magnitude of the effect is just dependent on the speed, not on the geometric size of the mass. That is, the effect is caused because the mass has a size, but its magnitude is independent of that size. That means that even a moving point mass will cause a similar extra gradient.