Does the age of the universe depend upon a specific choice of referential?

Question

Does the age of the universe depend upon a specific choice of referential or is there a way to define it in a referential-independent way?

Answer 1

There is a simple geometric interpretation of the quantity that is called the age of the universe.

Spacetime has a large-scale shape. It looks something like this:

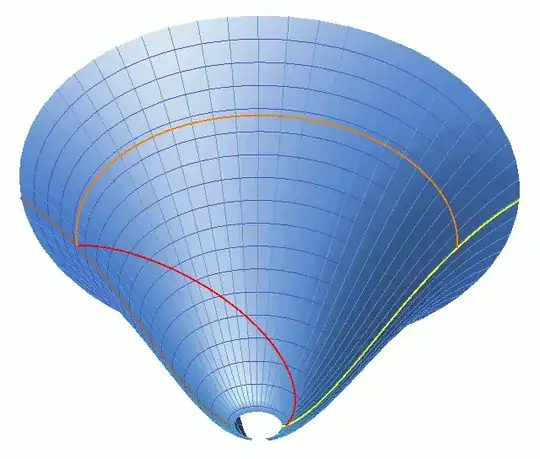
Later times are at the top, earlier times at the bottom.

You shouldn't take this too literally because it isn't a proper embedding (I flipped the sign of the metric to make it Euclidean, and embedded it in Euclidean space), and it's also somewhat misleading in other ways, but it gets one important thing right: spacetime is not maximally symmetric, the way a sphere is, but it does have a kind of "rotational" symmetry, like a pot made on a potter's wheel (though note that it doesn't actually circle back on itself at the distance suggested by this embedding).

On this diagram I drew "vertical" lines in light blue; the brown and yellow worldlines on the left and right are also lines in this category. The age of the universe at any point on the manifold is the distance to the big bang, or end of inflation, measured along one of these lines going through the point in question.

You could object that these lines are a coordinate grid, and indeed they are, but they're a coordinate grid singled out by the inherent shape of the manifold. If the manifold was more symmetric then there would be no natural coordinate system (you can't put polar coordinates on a sphere without choosing some poles). If the manifold was less symmetric then it also wouldn't select a natural coordinate system. But the actual shape of spacetime has the right amount of symmetry to select a preferred time coordinate which can be used to define the age of the universe.

The universe is not actually perfectly symmetric. If you zoom in, there are bumps on the surface, and this means there is some inherent fuzziness in the definition of the age at a point. But it is approximately equal to the distance measured when all of those bumps are smoothed out.

Answer 2

No. The age of the universe does not depend on any referential system. In order to measure time, you need some physical quantity that's changing to measure time against. In the case of cosmology, it's the time perceived by a typical observer based on the expansion parameter $a$ --see below. In a manner of speaking, it's the time that follows the galaxies in their mutual expansion. The mathematical basis is the FLRW metric of GR: $$ -c^{2}\mathrm{d}\tau^{2}=-c^{2}\mathrm{d}t^{2}+a(t)^{2}d\Sigma^{2} $$ where, $$ \mathrm{d}\mathbf{\Sigma}^{2}=\frac{\mathrm{d}r^{2}}{1-kr^{2}}+r^{2}\mathrm{d}\mathbf{\Omega}^{2} $$ and, $$ \mathrm{d}\mathbf{\Omega}^{2}=\mathrm{d}\theta^{2}+\sin^{2}\theta\,\mathrm{d}\phi^{2} $$ $k$ is the spatial curvature, $r$ is the actual distance between two galaxies, and $a\left(t\right)$ is called the expansion parameter, and represents the average separation of two standard galaxies measured in this cosmic time. The quantity, $$ H=\frac{\dot{a}}{a} $$ is the Hubble parameter, and represents how the scale factor changes with this cosmic time. The age of the universe is essentially the inverse Hubble parameter: $$ T=\frac{a}{\dot{a}} $$ And because the universe is large-scale homogeneous and isotropic, the words "typical observer" are justified, and this time does not depend on which observer you choose. Meaning: on which typical galaxy you sit and watch the universe expand. Now, we don't live in a FLRW universe. We live in a De Sitter universe (vacuum dominated), but the argument doesn't change (essentially).