Kruskal coordinates (in the context of extended black holes, or worm-holes) on a black hole geometry are defined, from the Schwarzschild coordinates ${\displaystyle (t,r,\theta ,\phi )}$, by replacing $t$ and $r$ by a new timelike coordinate ${\displaystyle T}$ and a new spacelike coordinate ${\displaystyle X}$:
$$T=\left(\frac{r}{2 G M}-1\right)^{1 / 2} e^{r / 4 G M} \sinh \left(\frac{t}{4 G M}\right)$$
$$ X=\left(\frac{r}{2 G M}-1\right)^{1 / 2} e^{r / 4 G M} \cosh \left(\frac{t}{4 G M}\right)$$
for the exterior region ${\displaystyle r>2GM}{\displaystyle r>2GM}$ outside the event horizon and:
$$ T=\left(1-\frac{r}{2 G M}\right)^{1 / 2} e^{r / 4 G M} \cosh \left(\frac{t}{4 G M}\right) $$
$$ X=\left(1-\frac{r}{2 G M}\right)^{1 / 2} e^{r / 4 G M} \sinh \left(\frac{t}{4 G M}\right)$$
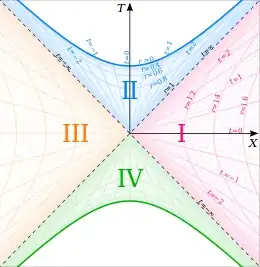
The picture above shows the Kruskal diagram, illustrated for $2GM=1$. The quadrants are the black hole interior (II), the white hole interior (IV) and the two exterior regions (I and III). The dotted 45° lines, which separate these four regions, are the event horizons. The darker hyperbolas which bound the top and bottom of the diagram are the physical singularities. The paler hyperbolas represent contours of the Schwarzschild $r$ coordinate, and the straight lines through the origin represent contours of the Schwarzschild $t$ coordinate.
The two diagrams below serve to understand how the two coördinate systems, $(t,r,\theta ,\phi )$, and $(X,T)$ are related. When, for example, a spherical lightwave (for which $r$ is a constant at any time $t$) is traveling towards the black hole, then you can see these waves as the concentric circles in the first picture (where $(x,y)$ represent $(r,t)$ and the angle refers to a Lorenz transformation, which is not important here).
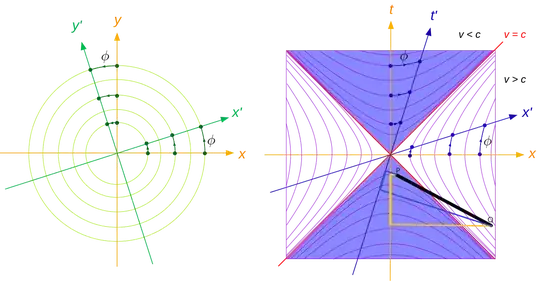
In the picture above you can see how the concentric waves travel in the Kruskal diagram. Observe that there is also a wave traveling in a downward direction. They travel backward in time towards the other black hole. Or forward in time from the other black hole. I.e., the other black hole represents a white hole. It seems as if the black and white hole have an infinite extent, but this is due to the coördinates. The waves end up at a point, the center of the concentric circles.
Maybe this gives you an idea.
There are no known physical circumstances that can lead to the existence of white holes. They are purely hypothetical (due to the math). Though Smolin says that they actually exist on the other side of black holes. The other side gives rise to other universes Smolin thinks some kind of a Natural selection "procedure" is happening. Likewise, he thinks that our big bang is similar to a white hole spitting out our universe, and as such there was a white hole geometry before the big bang. I'm not sure I understand this. Can time run backward?
To answer your question, it's very unsure if we live in a WH. Time runs back inside one. Of course, you can say that time runs backward in our universe or that we live on the other side of a black hole, as Smolin says, but there is no certainty.


