How to define a map from $\mathrm{SO}^+(1, 3)$ to $\mathrm{SL}(2, \mathbb{C})$?

Question

To explain how spinors transform under rotation people often use that $\mathrm{SL}(2, \mathbb{C})$ is a double cover $\mathrm{SO}^+(1, 3)$, that is there is a surjective homomorphism $\lambda:\mathrm{SL}(2, \mathbb{C}) \longrightarrow \mathrm{SO}^+(1, 3)$ with $\ker(\lambda)= \{-1,+1\}$ where $\ker$ means kernel.

I am not familiar with this but, apparently we can show, experimentally, using neutron interferometer, that if we rotate our measurement apparatus by an angle $2\theta$, then the spinor is rotated by an angle $\theta$.

Now by the last statement we should have a map from $\mathrm{SO}^+(1, 3)$ to $\mathrm{SL}(2, \mathbb{C})$. How can we define this map? By definition of a function each object has a unique image, so how can we define this map? Apparently the only way to solve this is to say for example that $2 \pi$ rotation and a $4\pi$ rotation are deafferents. Am I right?

Answer 1

Now by the last statement we should have a map from $\mathrm{SO}^+(1,3)$ to $\mathrm{SL}(2,\mathbb C)$. How can we define this map?

That's not quite right. What that statement says is that we should have a map from paths$^\ddagger$ on $\mathrm{SO}^+(1,3)$ to paths on $\mathrm{SL}(2,\mathbb C)$. In other words, if we start at some point $p\in \mathrm{SO}^+(1,3)$ and follow some continuous path $\gamma:[0,1]\rightarrow \mathrm{SO}^+(1,3)$, then we should be able to "lift" that to a path $\Gamma:[0,1]\rightarrow \mathrm{SL}(2,\mathbb C)$. This is indeed possible, provided we make a choice of starting point for $\Gamma$.

More precisely, let $h:\mathrm{SL}(2,\mathbb C)\rightarrow \mathrm{SO}^+(1,3)$ be our surjective homomorphism, let $\gamma:[0,1]\rightarrow \mathrm{SO}^+(1,3)$ be a continuous curve, and let $p\in \mathrm{preim}_h\big(\gamma(0)\big)$. Then there is a unique continuous curve $\Gamma:[0,1]\rightarrow \mathrm{SL}(2,\mathbb C)$ such that $\Gamma(0)=p$ and $h\circ \Gamma = \gamma$.

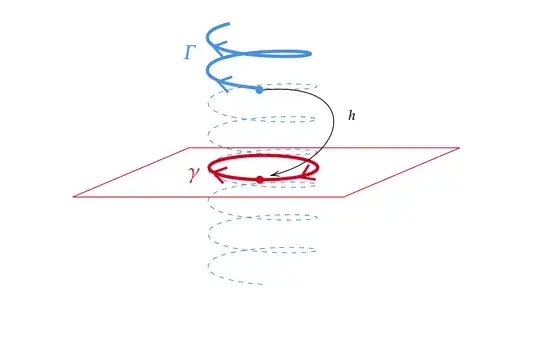
Explicitly, consider the following path through $\mathrm{SO}^+(1,3)$:

$$\gamma: [0,2\pi]\ni t \mapsto \pmatrix{1 &0&0&0\\0&\cos( t) & -\sin( t) & 0\\ 0 & \sin( t) & \cos( t) & 0 \\ 0 & 0 & 0 & 1}$$

Let $\Gamma(0) = \pmatrix{1 & 0 \\ 0 & 1}\in \mathrm{SL}(2,\mathbb C)$. Given the homomorphism which is explicitly written out in Jeanbaptiste's nice answer, we see that $\gamma$ lifts to the curve

$$\Gamma:[0,2\pi]\ni t \mapsto \pmatrix{e^{-it/2} & 0 \\ 0 & e^{it/2}}$$

It's straightforward to check that $h\circ \Gamma = \gamma$, but we observe that while $\gamma(2\pi)=\gamma(0)$, $\Gamma(2\pi)=-\Gamma(0)$.

---

$^\ddagger$Is the reason for you to say that we should maps path because, for example, to go from 0 to $2\pi$ we should go on a continuous path?

I think the confusion arises because we tend to think of rotations as continuous actions, like turning your experimental apparatus. But actually, a rotation is not a process, but rather the result of a process. In the language of my answer, a process is a path, and the resulting rotation is the endpoint of that path.

If you look down at a coffee cup and turn it $180^\circ$ clockwise, you obtain the same result as if you'd turned it $180^\circ$ counterclockwise. These two processes result in the same rotation of your cup, but they are clearly different processes. Similarly, turning your cup by an angle of $360^\circ$ results in the same rotation as not turning it at all.

When we hear statements like "a $360^\circ$ rotation sends a spinor $\psi$ to $-\psi$," we tend say to ourselves "wait, but a $360^\circ$ rotation is the identity transformation, so how does it change $\psi$ at all?" This confusion is a result of mistaking a process with its result. The process of continuously rotating a coffee cup by $360^\circ$ results in the same final configuration as the process of not touching the cup at all. But spinors and coffee cups are not the same. Rotations on the former are implemented by (representations of) elements of $\mathrm{SO}(3)$ while rotations on the latter are implemented by (representations of) elements of $\mathrm{SU}(2)$, and the aformentioned process does not have the same effect on spinors as the identity transformation does.

Incidentally, if you've ever turned a multi-turn knob you are already very familiar with this idea. If you turn the volume knob on a car stereo by $360^\circ$ to the right, the knob will have returned to the same configuration while the stereo system will not have. You may argue, "well yes, but the stereo has some internal degrees of freedom which shouldn't be expected to remain unchanged even though the external degree of freedom (i.e. the knob) has returned to its original configuration," but I'd counter with the fact that the same is true for fermionic particles, and the internal degree of freedom is precisely the spinor part of the particle's state.

Answer 2

The answer by Jeanbaptiste Roux contains the exact form of the mapping (Lie group homomorphism) from $\mathrm{SL}(2,\mathbb C)$ to $\mathrm{SO}^{+}(1,3;\mathbb{R})$ (the latter is also denoted in the literature as $\mathfrak{L}^{+}_{\uparrow}$ or $\mathfrak{Lor}(1,3)$). As a mapping, it is not bijective, so it does not an inverse in the proper mathematical sense (think of the function $f(x) = x^2 \vert f:\mathbb R\to\mathbb R^{+}$, where there is no $f^{-1}$), but, however, the equation

$$\Lambda^{\mu}_{~\nu} = \frac{1}{2}\mathrm{Tr}\left(\bar{\sigma}^{\mu}A^{\dagger}\sigma_{\nu}A\right) \tag{1}$$

can be "reversed" to

$$ \displaystyle{A=\pm\frac{\Lambda^{\mu}_{~\nu} \sigma_{\mu}\bar{\sigma}^{\nu}}{[\mathrm{det}\left(\Lambda^{\mu}_{~\nu} \sigma_{\mu}\bar{\sigma}^{\nu}\right)]^{\frac{1}{2}}}}\tag{2}$$

The proof of $(2)$ starting from $(1)$ is offered by Müller-Kirsten & Wiedemann on pages 70-71 of the first edition of the book. The proof should also be in the second edition, whose A m a z o n link I mentioned.

Answer 3

Let's define $\tilde{\sigma}^\mu \equiv \tilde{\sigma}_\mu$ the Pauli matrices, with $\sigma^0=\text{Id}$ that does not change when we raise or lower the index. There exist an $M$ isomorphism between the set of $2\times 2$ hermitian matrices and $\mathbb{R}^{1,3}$: \begin{align*} M : \mathbb{R}^{1,3} & \longrightarrow MH(2,\mathbb{C}) \\ x^\mu &\longmapsto C= x\cdot \sigma \end{align*} With $M^{-1}$ defined by: \begin{align*} M^{-1} : MH(2,\mathbb{C}) & \longrightarrow \mathbb{R}^{1,3} \\ C &\longmapsto x^\mu= \frac{1}{2} \text{Tr}(\tilde{\sigma}^\mu C) \end{align*} With the pseudo-norm given by $x \cdot x=\det C$. The matrices $C$ transform under $SL(2,\mathbb{C})$ according to the law $C \rightarrow A^\dagger C A=C'$. Since $\det C=\det C'$, we have the following equalities: \begin{align*} {x'}^\mu &= \frac{1}{2}\text{tr}(\tilde{\sigma}^\mu A^\dagger CA) \\ &=\frac{1}{2}\text{Tr}(\tilde{\sigma}^\mu A^\dagger \sigma_\nu A)x^\nu \end{align*} We then can define a relation between matrices from $SL(2,\mathbb{C})$ and $SO^{+}(1,3)$: \begin{align*} \phi : SL(2,\mathbb{C}) &\longrightarrow O^{+}(1,3) \\ A,-A & \longmapsto \frac{1}{2}\text{Tr}(\tilde{\sigma}^\mu A^\dagger \sigma_\nu A) \end{align*} Then $SL(2,\mathbb{C})$ is the double cover of $SO^{+}(1,3)$.

Answer 4

Since passive rotation and active rotation are equivalent, if we take the active point of view things should be more clear. What I mean is this : instead of taking the approach where it is the apparatus that is rotating we take the approach that is the spinor which is rotating.