I’m interested in semi-relativistic bound state, positronium, bottomonium, charmonium, etc.
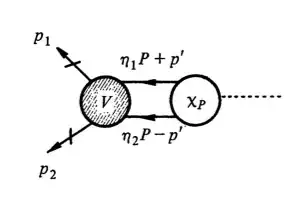
One way to treat such bound states in relativistic QFT is Bethe-Salpeter equation: $$(\Box+m^2)(\Box +m^2) \chi_{P}(x_{1},x_{2})+\int d^4z_1 d^4z_2 V(x_1,x_2;z_1,z_2)\chi_p(x_1,x_2)=0,\ \ \ (1)$$ where $\chi_p$ is Bethe-Salpeter amplitude and $V$ is Bethe-Salpeter Kernel. If we can solve this integral equation, we can calculate every observable in QFT by using the diagram as below:
There is another way to treat such semi-relativistic bound state, i.e. to define general two particle state using wave packets: $$|\psi>=\int \frac{d^3p_1}{\sqrt{(2\pi)^3E_{\bf{p_1}}}}\frac{d^3p_2}{\sqrt{(2\pi)^3E_{\bf{p_2}}}}f_1(p_1)f_2(p_2)|p_1,p_2>.$$ For example, when we think rest-frame positronium, its state can be written: $$|\text{Ps}>=\int \frac{d^3p}{\sqrt{(2\pi)^3E_{\bf{p}}}}\sum_{s,s’} f(p^2)Y_{lm}(\theta_p,\varphi_p)\sigma_{s,s’}b^{\dagger}(\textbf{p},s)d^{\dagger}(-\textbf{p},s’)|0>.\ \ \ (2)$$
These two ways are almost equivalent especially in lowest order calculation, so I guess there are some relationship between them. Does anyone know about such a relationship? In my opinion, Bethe-Salpeter amplitude $\chi(x_1,x_2)$ can match to the wave packets $f(p)$ or its square amplitude $|f(p)|^2$ in some approximation or limit, but I couldn’t find such an approximation.
$\textit{References}$
Itzykson and Zuber, $\textit{QFT}$, especially section 5-1-1, 5-2-3, and 10-2-1.