2

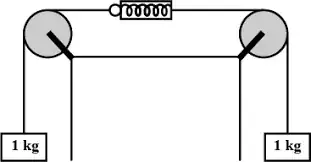
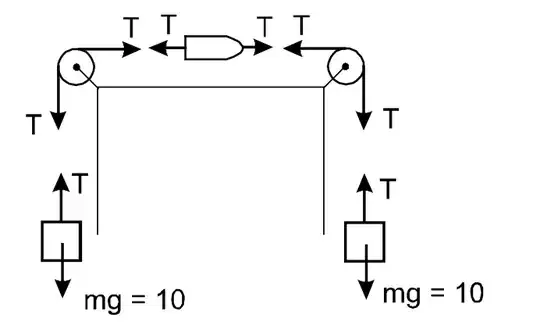
enter image description here

I have a question related to how the reading of the balance is equal to the tension of the string.

In my opinion, the reading of the balance should be twice as much as the tension. This is the diagram I drew:

enter image description here

Here isn't it very obvious that there are $2$ forces acting on the spring and pulling it in opposite directions, each with a magnitude $10N$? Therefore in my opinion, the reading $= 20N$.

But of course, it isn't so, the reading is $=10N$. I want to know what is wrong in my reasoning.

Community
  • 1

2 Answers2

3

This problem depends quite a bit on knowing how the balance is calibrated. Take the force diagram you've drawn here and compare it to the "normal" case in which the balance is attached to the ceiling and has a weight hanging on the bottom, which is a situation in which we know that the balance is supposed to read the weight of the object.

jwimberley
  • 3,911
3

Imagine the balance is attached to the ceiling by a string and a $10$ N mass is hung from the other end. You would say the reading on the balance is $10$ N. Neither the balance nor the mass is not accelerating.

Consider a free-body diagram of the balance. The string attached to the ceiling is pulling up with some magnitude force, $F_1$. The string attached to the $10$ N mass is pulling down. You should be able to calculate what $F_1$ is. That should tell you about your situation and how spring balances work.

Bill N
  • 15,522