Could the observable universe be bigger than the universe?

Question

First of all, I'm a layman to cosmology. So please excuse the possibly oversimplified picture I have in mind.

I was wondering how we could know that the observable universe is only a fraction of the overall universe. If we imagine the universe like the surface of a balloon we could be seeing only a small part of the balloon

or we could be seeing around the whole balloon

so that one of the apparently distant galaxies is actually our own.

In the example with the balloon one could measure the curvature of spacetime to estimate the size of the overall universe, but one could also think about something like a cube with periodic boundary conditions.

Is it possible to tell the size of the overall universe?

---

_{Artistic image of the observable universe by Pablo Carlos Budassi.}

Answer 1

Yes, it's possible in principle that we see the same galaxy more than once due to light circling the universe. It wouldn't necessarily be easy to tell because each image would be from a different time in the galaxy's evolution.

There is a way to test for this. The cosmic microwave background that we see is a 2D spherical part of the 3D plasma that filled the universe just before it became transparent. If there has been time for light to wrap around the universe since it became transparent, then that sphere intersects itself in one or more circles. Each circle appears in more than one place in the sky, and the images have the same pattern of light and dark patches. There have been searches for correlated circles in the CMB pattern (e.g. Cornish et al 2004), and none have been found.

Answer 2

Another possibility (to complement the existing answers) is that space could be finite in some directions but infinite in others, like a cylinder.

References, for a theoretical approach:

• Lachieze-Rey & Luminet (1995), "Cosmic topology". This is an 80-page review
• Ellis (1971), "Topology and cosmology".

Answer 3

1. "I was wondering how we could know that the observable universe is only a fraction of the overall universe."
2. "Is it possible to tell the size of the overall universe?"

The first step in knowing (1) and/or (2) is to know whether the universe is infinite of finite. At the present time this is not known with any high level of confidence. In a few decades I think it is likely cosmologists will know with a reasonable level of confidence.

If the universe is infinite then it is clear that it is bigger than the observable universe which is finite.

If it becomes known that the universe is probably finite it is likely it will also be known that the value of the curvature density (represented by $\Omega_k$) will be known to be in a range of values with a confidence level like 95%. If the entire 95% range has all values < 0, say between -a and -b. then it will be known with a reasonably accurate probability distribution that the radius of curvature will have a positive value within a corresponding range of some billions of light years.

Regarding the title question, if the radius of curvature is R, and the radius of the observable universe (OU) is r, then the most distant point from an observer is $\pi$ R. If r = $\pi$ R, then you are seeing a point as far away as any exists. If r > $\pi$ R, then you are seeing the same point that is closer to you in the opposite direction. If what you are seeing is the CMB, you will only be able to see a point in it which is closer than the same point in an opposite direction. However, if r is sufficiently less than $\pi$ R, no point in the observable universe would be old enough to be the CMB emitting surface. This would then make it clear to the observer that r > $\pi$ R.

Answer 4

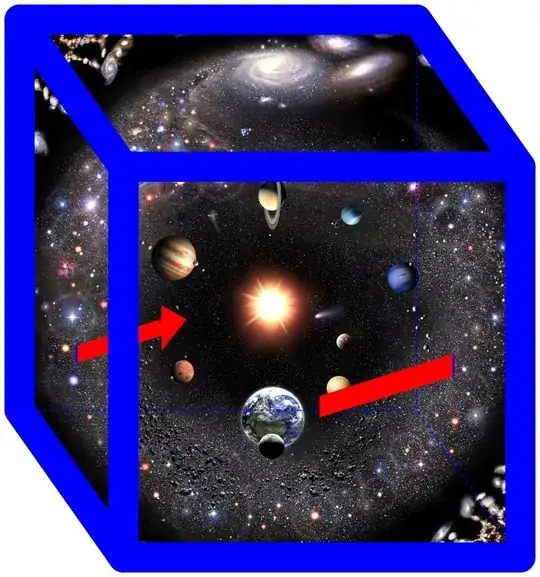
Another answer has explained the evidence that the observable universe does not wrap around and meet itself on the other side, in that the telltale signs do not appear to be there. However that answer only addressed a curved Universe, see below.

But how can we be confident that there is not an exact match, or that we cannot see almost all of it?

One argument is based on the assumption that there is nothing special about the present moment. The horizon of the observable universe arises because of the limited time its light has had to reach us. As time passes, more light from beyond the horizon will finally make it here and the horizon will recede accordingly. Assuming that this process is ongoing, there is no reason to suppose that we are, as yet, any where near the end of it.

Another argument is touched on in yet another answer, which hinges on the curvature of space. It is less than our ability to detect, or to put it another way, it is so nearly flat that we cannot tell the difference. If we could see almost all the universe, and it was a simple 3-sphere the way your pictured balloon is a 2-sphere, then it would be noticeably curved. But it is wrong to take the 3-sphere as the only possible shape. If you inflate a donut-shaped balloon, such as a plastic life preserver, its intrinsic (overall or average) curvature is always zero. A donut universe would always have zero curvature, no matter how much of it we could or could not see. But the topology of space (i.e. the correct solution to the equations of General Relativity) is unknown. We have no reason whatsoever to choose the sphere over the donut, indeed some models point to a hyperbolic space - which must be either infinite or with multiple "handles" like a higher-dimensional pretzel. So, despite many popular claims to the contrary, the apparent near-flatness of the Universe actually tells us very little.

In a simple toroidal Universe, geodesics are straight lines. If it were smaller than the observable scale then such lines would appear to repeat the distribution of mass/energy endlessly with a period of one Universal span. We would see the Universe beginning to repeat itself, like a stack of identical cubes. This was searched for many years ago and was found lacking, however our ability to observe great distances was limited by the technology of the day.

Since then we have mapped the CMB. But this does not help immediately, as the source of the CMB is just a 2-sphere (i.e. not a geodesic) at an arbitrary (time-dependent) and expanding distance away. Its apparent size is the boundary of the observable universe at that moment. The problem of relating such a busily-expanding sphere to the scale of a toroidal Universe is neatly illustrated in this video. (Note that the apparent reflections at the edge are an illusion, they are actually the other side coming across from the neighboring cube.) As far as I know, nobody has searched for such subtleties since that decades-old optical search (I'd love to hear if they have!).

And there are many other candidate shapes besides infinity, spheres and donuts. Each has its signature pattern of geodesics. For a good introduction see Jeffrey R. Weeks; The Shape of Space, CRC, 2002.

Answer 5

We could discover that the actual universe is larger than the observable universe when there is a non-zero constant curvature everwhere. Then, this would be like standing upon the earth and seeing as far as the horizon. In the picture drawn above what we can observe would be limited by a kind of cosmological horizon.