Is the Bohm-Aharonov effect a proof of real $U(1)$ local gauge transformations "taking place" (instead of being just a math procedure)?

Question

Under a local gauge (phase?) transformation of the field operator for electrically charged fields, $\psi \rightarrow e^{\mathrm{i}\phi(x_{\mu})}\psi$, where $e^{\mathrm{i}\phi(x_{\mu})} \in U(1)$, the associated $\mathcal{L}$ remains invariant if we add an electromagnetic potential $A_{\mu}$ to it.
(If instead of performing a local gauge transformation we perform a global one, $\psi \rightarrow e^{\mathrm{i}\phi}\psi$, then no four-potential $A_{\mu}$ has to be added to the Lagrangian to keep it invariant under this transformation. This transformation is, via Noether's theorem, associated with the conservation of the number of particles (or "conservation of probability") and thus electric charge).

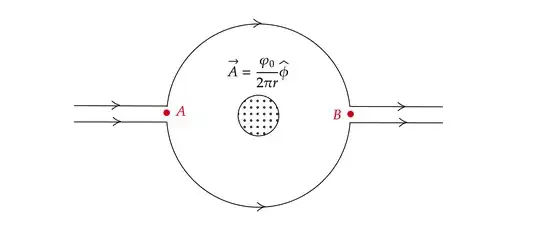
All neat and well. Now, look at the shifted pattern of the double-slit experiment. Can we reason in the other direction too? Can we say that if we physically make a four potential $A_{\mu}$ appear (in this case only the space part is present) appear, as in the experiment, that this causes the shift in the diffraction pattern? Does this field, which is constant, induce, indirectly, a global transformation on the pattern? Or, directly, a local gauge transformation on the electron field (states)? It looks as if the pattern is globally phase transformed. This means that the electron-field "in-between" is globally transformed too. Is the four-potential inducing phase-shifts on the electron field between slits and screen? Thereby making some paths more and some paths less probable (in the path integral formulation)? Note that the diffraction pattern moves in the other direction if the current inside the solenoid is reversed.
So it seems as if the global phase transformed pattern stands in direct relation to locally transformed electron states. Can we say these states are not gauge transformed at random (as in the mathematical procedure of imposing a local gauge transformation on the charged field which makes an $A$-field show up) but as a result of the $A$-field (which is cylindrical symmetric and constant in time)?

Or stated in still another way: can we say that instead of the fact that a local gauge transformation gives rise to an $A_{\mu}$ field the reverse holds, namely that an applied $A_{\mu}$ field gives rise to real local phase transformations? Moreover, in the face of quantum fields mapping spacetime points to operators, this doesn't seem unreasonable.

I found some new information on this subject:

4.3 The Aharonov-Bohm effect The Aharonov-Bohm effect (Aharonov and Bohm, 1959) deserves special attention since it is often considered to be an instance of the Berry phase. The scenario is very well known: a split electron beam passes around a solenoid in which a magnetic field is confined. The region outside the solenoid is field-free, but nevertheless, a shift in the interference pattern on a screen behind the solenoid can be observed upon alteration of the magnetic field. The phase shift can be calculated from the loop integral over the potential, which—due to Stokes’ theorem—relates to the magnetic flux,...etc.

More can be read here, where the Berry phase is discussed. Somehow this seemed important for this problem. I don't know exactly how though.

Answer 1

I'm not sure this is all directly relevant to your question, but it is a good opportunity to clarify a few issues.

• It is useful to distinguish between a gauge transformation and a physical, or symmetry transformation. A gauge transformation, whether local or global, is just a relabelling of your coordinate system or measurement scale. Sometimes this is called a passive transformation. It is just the same as choosing to measure in Fahrenheit or Celcius, or saying the week starts on Sunday or on Monday. By definition nothing physical can change due to or depend on this choice.
• How does a symmetry transformation differ from a relabelling? You can only define this with respect to some reference. So whether magnetic field in complete isolation is pointing to front or back is just a coordinate choice, but if this magnetic field lives on Earth, then its field has some orientation with respect to the reference field of Earth. You can now try to establish how certain transformations change or don't change your magnetic field, with respect to the reference.
• Quantum mechanics has this peculiar feature that the phase of the wavefunction is not observable. In other words: there is no reference in the universe with respect to which we can denote phases of wavefunctions. The same happens in spontaneous symmetry breaking: the value of the superfluid order parameter is rigid, but can only be defined with respect to another superfluid. (Confusingly, sometimes this (broken) symmetry is called global gauge symmetry, but that's just outdated, confusing, and basically wrong.)

Now, I suspect that you think that the position of the central peak of the interference pattern is related to the actual value of the phase (if we were to define this with respect to some reference). Then if you shift the phase field $\phi(x) \to \phi(x) + \alpha$ by a global transformation (whether or not with respect to the reference), then the peak will also be shifted. You say: "Clearly, the pattern on the screen has undergone a global phase transformation".

But this is not the case. The interference pattern arises due to, well, interference, so in your picture between $\psi_1$ and $\psi_2$. Peaks appear where $\phi_1(x) - \phi_2(x) = 0 \mod 2\pi$. A global transformation, by definition, shifts the wavefunction the same way at every point. The interference pattern is therefore not affected by global transformations, even if these were physical transformations with respect to some external reference wavefunction.

This should be sufficient to understand why global transformations have no effect on the interference pattern. But, regarding your constant vector potential $A_\mu(x) = A_\mu \forall x$, you can also trivially see that $\oint \text{any constant} = 0$, and you can always write the accumulated phase difference as some closed contour integral.

Answer 2

A full analysis of the Aharanov-Bohm effect in the double slit experiment is beyond the scope of this answer, but the idea can be understood from a toy model. Consider the following setup:

Imagine electrons confined to move along two wires as shown, but which are otherwise free. They're drawn separately so as to be visible, but we are imagining them to be infinitesimally close together. The dotted region denotes the interior of the solenoid (the only place where the magnetic field is nonzero); in the exterior, the vector potential is given by $\vec A = \frac{\varphi_0}{2\pi r}\hat \phi$, where we've chosen to use the Coulomb gauge.

We now ask about the phase acquired by each "beam" of particles as they travel from $A$ to $B$ along their respective paths. If $\varphi_0=0 \implies \vec A = 0$, then the two 1D plane waves would take the form $$\psi_{\uparrow}(\ell,t)=\psi_{\downarrow}(\ell,t) = \psi_0 e^{i(k\ell - \frac{\hbar k^2}{2m} t)}$$ where $\ell$ is the distance traveled along the wire. Since the distances are the same for the top and bottom path, the two beams which left $A$ in phase are also in phase when they meet again at $B$.

If $\vec A \neq 0$, this is no longer true; each state acquires an additional phase factor given by $e^{i\gamma} = e^{ie\int \vec A \cdot d\vec r}$, where the integrals are taken over the respective paths. Integrating over the bottom path yields

$$\gamma_\downarrow = e\int_{-\pi}^0 \frac{\varphi_0}{2\pi R} (r d\phi) = \frac{e\varphi_0}{2}$$ $$\gamma_\uparrow = -\frac{e\varphi_0}{2}$$ which means that if the two beams started in phase at point $A$, their phase difference at $B$ is given by $$\Delta \gamma = \gamma_\downarrow - \gamma_\uparrow = e\oint \vec A \cdot d\vec r = e\varphi_0$$ where this (closed loop!) integral is taken over the entire circle in the counterclockwise direction. It is this phase difference which leads to interference, depending on the value of $\varphi_0$.

If you'd like to change the gauge, you are welcome to do so - gauge transformations are basically passive coordinate changes, albeit in a somewhat abstract sense. We multiply each wavefunction by $e^{i\alpha(\vec r)}$ and add $\nabla\alpha$ to the vector potential. The extra factor of $e^{i\alpha(\vec r)}$ clearly doesn't affect the phase difference between the two beams at any individual point because - since $\alpha(\vec r)$ is being evaluated at the same point - the two beams are (locally) phase-shifted by the same amount. The phase difference acquired as they traverse their respective semicircles is also unaffected because

$$\Delta \gamma = e \oint (\vec A + \nabla \alpha) \cdot d\vec r = e\oint \vec A \cdot d\vec r$$ where we've used that $\oint \nabla \alpha d\vec r = \alpha(\vec r_f)-\alpha(\vec r_i) = 0$ for any scalar function $\alpha$ (as an obvious consequence of starting and ending the integral at the same place). As a result, the relative phase between the two beams which are in phase at $A$ is unaffected by a change of gauge (as it must be).

Can we say that if we physically make a four potential $A_\mu$ appear (in this case only the space part is present) appear, as in the experiment, that this causes the shift in the diffraction pattern?

Yes, the presence of a non-zero vector potential causes the shift in the diffraction pattern.

Is the Bohm-Aharonov effect a physical proof of real U(1) local gauge transformations being performed (and not merely mathematical)?

Turning the solenoid does not result in a gauge transformation. Gauge transformations are by their very definition mathematical; they exploit redundancy in our description of nature. Two configurations which are related to one another via gauge transformation are physically identical in every way.

When you turn the solenoid, $A_\mu$ changes, because the electromagnetic fields change - but this isn't a change of gauge (which by definition would not change the fields). In other words, the $A_\mu$ at time $t=0$ before you switch on the solenoid and the $A_\mu$ after you turn on the solenoid are not related to one another by a gauge transformation.