I know, I know, reference frame and shit. But, I am asking which one are we calculating? When we are calculating we are using Euclidean Geometry. So how should we think about it in form of Spherical Geometry?
For example, there are two cities A and B. They both lie in the same longitude. So which path is the displacement, the yellow one or the blue one?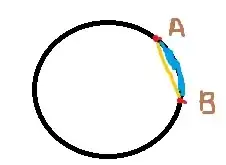
- 133
2 Answers
I would summarize that it is a bit the matter of convention. Quick side note: Displacement, to my mind as a condensed matter physicist, is actually the distance with respect to some reference point, so the displacement of city $A$ relative to city $B$ seems a somewhat odd quantity. You can give it a mathematical sense if you refer it to a path, that is the final displacement an object experienced when it travelled from city $A$ to city $B$ by some arbitrary path. Cf. wikipedia, https://en.wikipedia.org/wiki/Displacement_(geometry)
Pedantry aside, the displacement has something to do with the geometry you imprint on your system. When you embrace $\color{blue}{\textrm{spherical geometry}}$, the displacement is the $\color{blue}{\textrm{blue line}}$ in your sketch. That is the shortest path you can take when you restrict yourself to moving along the surface of the earth.
If you had a powerful drill, you might not want to accept the metric of the sphere. In the geometry appropriate to the motion with a drill ($\color{orange}{\textrm{Euclidean geometry}}$), the $\color{orange}{\textrm{yellow line}}$ is the displacement.
So, in the end, both options are available, they correspond to different underlying geometries, and it is your description of the problem and the kind of question you want to ask that leads you to decide on a specific geometry.
- 1,346
@Blank you seem to be referring to distance on a map of places on the earth's surface. If things get bigger than relatively local area maps, its better to think of a geodesic along the earth's surface which is the equivalent of a "shortest distance" along the surface of a sphere.
Map making is pretty complex in practice with lots of trade-offs because things like distance, angles etc get distorted in going from curved surface to a flat plane. The way cartographers usually make local area maps with some distance scale (I think what you mean by displacement) is to tack an ellipsoid to some known reference point on the earth's surface (a benchmark). The ellipsoid is a best fit over some limited area to that piece of earth-surface. They then choose a projection method onto a plane and preserve more or less the surface distances that really exist on the actual earth's surface. So in your sketch they are usually trying to preserve the distance along the surface (blue) on the flat map.
- 65