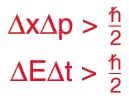Would the Heisenberg uncertainty principle give mass to massless particles?

Question

Background

I am self-studying QFT and I was learning about the Higgs field (lectures 7 - 8 in the link), and I learned how massless particles behave in the Higgs field. What I saw was that they follow this equation:

$$\Phi = fe^{i\alpha }$$

Where $f$ is the fixed magnitude of the field at the main circle of the potential (the bottom of it), and $\alpha$ is the rotation around this circle. Massless particles move around this main circle by slowly varying $\alpha$.

I learned that mass is the QF that oscillates back and forth when you displace it everywhere simultaneously homogeneously, and there is a restoring "force" that wants to bring it back in place that causes it to oscillate. Massless particles are the opposite, they have no restoring "force" that brings it back when you displace it, and therefore do not have mass.

---

The Question

A consequence of the Heisenberg uncertainty principle is that nothing can ever standstill or not oscillate. Everything has to oscillate.

With this consequence, then, would it make sense that massless fields would oscillate too like the mass fields? Would this give everything mass, or is there something critical that I am missing here, like misunderstanding the Heisenberg uncertainty principle?

Answer 1

A consequence of the Heisenberg uncertainty principle is that nothing can ever standstill or not oscillate. Everything has to oscillate.

I do not think this is a correct deduction. If one measure momentum there is a limit to the accuracy of measuring position , is all that the HUP says. It is an envelope where measurerements of momentum and position at the same time have to be. Nothing about oscillations there.

Also, quantum mechanics is a probabilistic theory, many measurements under the same boundary conditions must be carried out to get a probability distribution that can be checked against calculations.

The HUP

defines a probability for the variables to fluctuate, the fluctuations due to the uncertainty are in the probability distributions, a probable state to exist, but it is not oscillating in space time,(or energy-momentum) as it is the wavefunction that has the wave behavior. In space time there is just a probability of measurement that can be calculated. ( example: orbitals not orbits).