Intuitive question about torque formula

Question

Consider two objects as shown:

On one side a box with mass 1 kg, 2 m apart from pivot and on the other side two boxes of mass (1 kg each), 1 m apart from pivot, balance a seesaw.
This is the question: Why, intuitively, the two squares (on the right hand side) must be exactly one meter apart from pivot and not for example 1.03 m in order to balance the seesaw? In other words why, intuitively, torque is equal to force times distance; (and the relation is linear); I mean it's
$$T=mgd$$
And not for example:
$$T=m^{1.006}gd^{1.07}$$

Answer 1

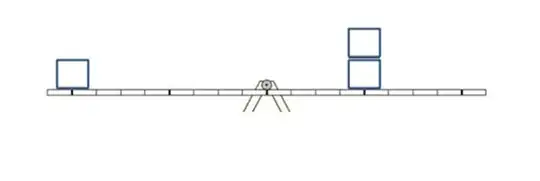
That is a deep question actually.

The tldr answer is that the center of gravity of all the boxes must be over the pivot for balance. And you calculate center of gravity with the weighted sum of the individual weights.

$$ \text{(center)} = \frac{ \sum_{\rm all} \text{(position)*(weight)} }{ \sum_{\rm all} \text{(weight)} } \tag{1}$$

_{The term weighted sum in mathematics comes exactly from this operation in physics. The weight describes how important each position is.}

But the above is kind of a circular argument, as here in the numerator we have $\text{(position)*(weight)}$ which is exactly what you are asking about. Why the multiplication.

The mathematical answer is that the above equals to the sum of each fractional contribution of position. Each fraction being the individual weight to the total weight (and thus the term weighted average).

$$ \text{(center)} = \sum_{\rm all} \text{(position)} \left( \frac{\text{(weight)}}{\text{(total weight)}} \right) \tag{2}$$

---

The long answer is that each force acts along a line, and when two or more forces add up together there are some rules of geometry that dictate where the resultant force acts though. You learn in high school how to add vectors by placing them on the same origin, which yields the correct magnitude and direction, but this is not sufficient to find out where the resultant acts.

So for two non-parallel forces acting through separate points, A and B as seen below the process involves 4 steps.

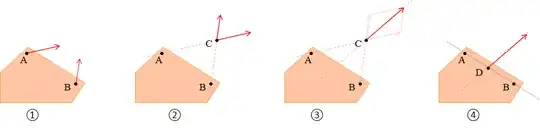
1. Slide each force along their line of action until the forces meet at a point C.
2. Combine the forces vectorially (component by component) on the common point.
3. Describe the new line of action of the combined force as parallel to the combined force and through the point C.
4. (optional) Slide the combined force along its line of action, back to wherever makes more sense for the problem at hand. For example on the line connecting the two original forces to new point D.

_{Note with force vectors you are free to slide them along their line of action without changing the problem at hand.}

So what happens when the two forces are parallel? Well follow the same process as above, but the point where they meet is at infinity (on the horizon) and when you do the final step #4 the point D ends up being mathematically at the weighted sum of the two original forces.

The same argument as above can be done algebraically instead of geometrical by considering the torque about the pivot. Torque is the numerator of expression (1) and the geometry of the problem introduces the concept of a moment arm of a force. This means that only the perpendicular distance counts.

$$ \text{(torque)} = \text{(distance)} * \text{(force)} \tag{3a} $$

or in vector form

$$ \vec{\tau} = \vec{r} \times \vec{F} \tag{3b} $$

Balance happens when the sum of all the torques are zero, which has the geometric interpretation that the combined force line of action goes through the pivot.

Answer 2

You may not find conservation of energy any more intuitive than torque, but if you're willing to grant that perpetual motion machines are impossible, there is no way the ratio of distances for balance could be anything other than the inverse of the ratio of weights. For any other ratio, you'd be able combine multiple seesaws, and the ability to move boxes horizontally from one seesaw to another, to lift boxes vertically "for free".

Answer 3

I don't think there is an intuitive explanation, because if we could measure with a great precision we would see that $m_1d_1 \neq m_2d_2$ indeed.

The expression above is valid in the approximation that the earth radius is so big compared to the distances of the scale that the force of gravity can be considered parallel.

But in reality, that forces have the direction of the center of the earth, and are smaller for bigger distances, considering a straight arm. The force acting at the end of it is smaller than that acting closer to the pivot point.

So you are right about the slight difference from the standard expression.

Answer 4

You can consider this from an energy balance perspective. A circle of twice the radius has twice the circumference, so if the seesaw moves, an object that's 2m from the fulcrum moves twice as far as an object that's 1m from the fulcrum (vertically, horizontally, or along the arc). An object's change in potential energy is proportional to its mass and vertical displacement, so a object that moves some distance vertically has the same change in energy as an object that weighs half as much but moves twice the distance, or an object that weighs twice as much but moves half the distance.

From this, you can see that when you have an 1 kg object at 2m and a 2kg object at 1m, moving the seesaw results in a perfect energy balance. Systems tend to spontaneously move into states with lower energy, like how an imbalanced see-saw will tilt until the higher-torque end is sitting on the ground. In the case of a balanced see-saw, moving the see-saw results in no overall change in potential energy at all, so there is no preference for the see-saw to move in one direction or the other, meaning there is no impetus for it to move at all. If you have two weights of fixed mass and fix the position of one of them, there is exactly one place you can put the other weight in order to achieve balance. If you put it anywhere else, the seesaw will seek to lower its potential energy by tilting.

This perhaps moves the goalposts from "why is torque linear" to why is "why is potential energy linear", but that might be a little more intuitive. It comes down to the fact that in a uniform gravitational field, altitude doesn't affect the amount of work you need to do to climb higher - moving from 0m to 1m takes exactly the same amount of work as moving from 1000m to 1001m. This should be intuitive from the fact that the zero point is entirely arbitrary - there's no reason you couldn't define the 0m to 1m change as actually being a 1000m to 1001m change, and the 1000m to 1001m change as a 2000m to 2001m change. If this relationship wasn't linear, the work required to climb higher would depend on your altitude, which you could redefine simply by changing your reference frame. But clearly, choosing a different reference frame cannot change the amount of work required to do something.