What is the role of wave packets in LSZ formulae?

Question

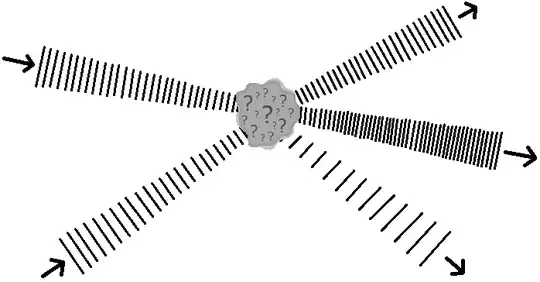
When deriving LSZ formulae, we assume asymptotic particles’ creation/annihilation operators as: $$a_\text{g,in/out}\ \ (\mathbf{p})\equiv \int d^3k \ g(\mathbf{k}) a_\text{in/out}(\mathbf{k}), \ \text{where}\ \ g(\mathbf{k}) =\exp\left(-\frac{(\mathbf{p} - \mathbf{k})^2}{2\sigma^{2}}\right).$$

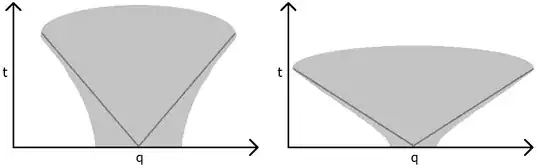
This is because to get such normalized initial/final states as can define weak convergence of asymptotic creation/annihilation operators, and to ignore the interaction between different particles in initial/final states. However, after computing the LSZ, $g(\mathbf k)$ term is ignored by taking the limit of $\sigma \rightarrow 0$ & integrating about $\mathbf{k}$.

Here are some questions.

1. Why can we ignore $g(\mathbf{k})$ in LSZ? I think such the limit abandons spacial localization of particles at initial and final state and it makes particles interact even in the initial state.
2. Even if such the limit is physically correct, what is the difference between assuming the localized operator $a_\text{g,in/out}(\mathbf{k})$ or not. In other word, why should we introduce the $a_\text{g,in/out}(\mathbf{k})$ even though we make wave packets collapse anyway by taking the limit $\sigma \rightarrow 0$ at the end of derivation?
3. What is the difference between simply taking plane waves as an asymptotic state and to get plane waves by collapsing wave packets? When we take the limit $\sigma \rightarrow 0$, I think wave packets correspond to delta function, so it seems meaningless to define $a_\text{g,in/out}(\mathbf{k})$ and its spatial locality.

I have already read this post and this post, yet never understood clearly.

References

1. M. Srednicki, QFT ; chapter 5.

2. Peskin & Schroeder, QFT; sections 7.1-7.2

3. Wikipedia, LSZ reduction formula

Answer 1

Herein lies the rub of the whole wave packets rigmarole.

One might say that as the frequency uncertainty $\sigma \to 0$, the wavepacket gets less localized in space, eventually becoming a true plane wave. So why not just start with $\sigma = 0$ at the beginning? Why take the limit?

The thing is, it's not strictly true that wave packets become more localized as $\sigma \to 0$!

Imagine a wave packet with average momentum $\vec{k}_0 = \vec{0}$ which starts at some position $\vec{q}$ at $t=0$. Imagine what happens when $\sigma$ the frequency uncertainty gets larger, meaning the initial position space uncertainty gets smaller. This is depicted above. Here the gray region is the region where the absolute value of the wave packet is within one standard deviation of the average. As the initial position space uncertainty gets smaller, the momentum space uncertainty gets larger! This means the envelope spreads out faster, because the range of possible momenta is larger.

This is why the wavepacket depicted on the left has a larger initial spatial uncertainty, but after a bit of time its the picture on the right which has a larger position space uncertainty. (The dark gray lines are the wordlines the particle would travel if it had a momentum of $k = \pm \sigma$.)

People often say that the Heisenberg uncertainty relation says that more position uncertainty implies less momentum uncertainty. However, this is just a lower bound. At late times, the picture on the left has both a smaller momentum uncertainty and a smaller position uncertainty!

Let me now introduce the concept of the "interaction zone." The way you are supposed to think about scattering is that the particles come in from infinity, interact in some large region of space called the "interaction zone," and then some particles leave.

The interaction zone is the gray region in the picture above. So, as we take $\sigma \to 0$, our "beams" of particles (the waves entering and leaving the interaction zone) actually become sharper and sharper, and begin to look, from a distance, more and more like straight lines. However, the interaction zone itself is actually getting larger and larger! When you are integrating over $\int d^4 x$ in the LSZ reduction formula, in a way you are really integrating over this interaction zone, which gets spatially larger as $\sigma \to 0$. However, due to the order of limits you are taking, there is in a way a larger zone beyond the interaction zone, maybe called the "scattering zone," where your particles shoot in and out in thin beams.

This is the reason for carefully constructing asymptotic states in the LSZ reduction formula using wavepackets.