Distance between particles in pair annihilation (or any other matter antimatter collision)

Question

Imagine a pair of electron and positron colliding in pair annihilation process, which produces two gamma photons: $$e^+ + e^- \longrightarrow \gamma + \gamma $$ My question is that what exactly happens when two particles reach to each other. In other words, does the distance between them come to zero? If not, how does this relate to Heisenberg's uncertainty principle?

Answer 1

First of all the interaction of elementary particles is in the realm of quantum mechanics. Quantum mechanics is a probabilistic theory, it allows to know the probability of an interaction happening. Probability imposes the need to measure the same interaction with the same boundary conditions many times, so a distribution can be checked against the data. So no distance can be defined between two particles,just a probable distance.

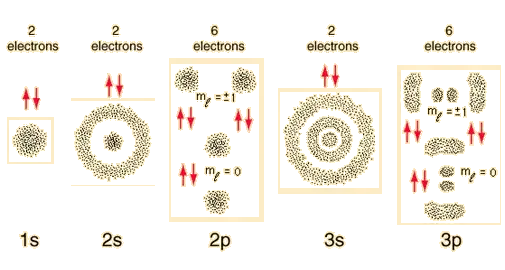
This can be clearer when discussing orbitals, not orbits, for atomic electrons. Look at these orbitals allowed for the hydrogen atom:

Each little dot is an allowed position to be occupied by an electron, and note the number of positions that exist for the central part where the proton is sitting.

Similar orbitals mathematically exist for the positronium, where in contrast with the hydrogen atom, where quantum numbers do not allow annihilation, when the electron orbital hits the positron, annihilation happens. One calculates the probability of this happening using the quantum mechanical equations needed for the particular problem.

For a rule of thumb, Heisenberg's uncertainty principle allows to have an envelope of available locations in space depending on the momenta. Heisenbeg's uncertainty comes from the commutation relations of variables entering the calculation of particle interactions, and these relations become mathematically clear when learning QFT.

Answer 2

Before annihilation the electron and positron form an hydrogen like object called positronium. In positronium the electron and the positron occupy the same orbital and there is a finite probability that they are at the same location. Quantum mechanics does not allow a more precise statement on the relative position of the two particles.