Intuition for angular momentum

Question

A single object with mass $m$ is rotating around an origin at a distance $r$ and speed of $v$; so its angular momentum is equal to $mrv$; if we decrease its radius (say shorten the rope) its speed increases, due to conservation of angular momentum. What I try to understand, intuitively, is what the radius has to do with this increase in speed.

For a more detailed description of what I mean, consider an example of linear momentum: an object with mass $m$ and speed of $v$ has linear momentum of $mv$. If it faces and sticks to another object with mass $m$ and speed of zero its speed decreases to half; here it's easy to understand, intuitively, that why (the increased) mass decreases speed; but in case of angular momentum it's not easy to understand, intuitively, why for example an increase in radius of an object, decreases its speed.

Answer 1

About increase of angular velocity when radius of circumnavigating motion is decreased.

The diagram below represents the trajectory of a point mass that is circumnavigating a central point, in the process of being pulled closer to the central point.

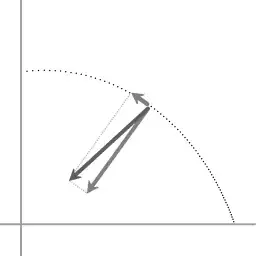
The dark gray arrow points represents the centripetal force that the point mass is subject to.

If the centripetal force would be precisely the required centripetal force to sustain circumnavigating motion then the radius of circumnavigation would remain constant.

Here there is a surplus of centripetal force. The dotted line represent the trajectory through one quadrant, and this motion is not circular; the mass is being pulled inward, so the motion is more like an inward spiral.

If the motion would be circular the centripetal force would be perpendicular to the instantaneous velocity. But the motion isn't circular.

In the diagram the total centripetal force is decomposed in two force components: one component perpendicular to the instantaneous velocity, one component tangent to the instantaneous velocity. The tangent force component is in the process of increasing the instantaneous velocity. In other words: during the contraction the centripetal force is doing work

The amount of work that the centripetal force is doing is such that when the radial distance is halved the angular velocity is quadrupled.

Here is a comparison to underline that in order to understand change of velocity you have to identify the force that is doing work.

For illustration I will first discuss change of linear velocity, with a deliberately wrong "explanation".

When a cannon is fired the projectile flies out of the cannont and the cannon recoils. This happens because momentum must be conserved. The projectile flies out of the cannon because of the recoil of the cannon, and the cannon recoils because the projectile flies out of it.

Clearly the above is nonsensical.

As we all know: to explain the change of velocity we must identify the force that is involved. The explosion of the charge creates a hot, high pressure gas, the expansion of that gas is doing work, causing the projectile to shoot out of the barrel and it causes the recoil.

The same principle applies in the case of angular acceleration. When there is a surplus of centripetal force the system will contract, during that contraction the centripetal force is doing work, causing angular acceleration.

Conversely, if the centripetal force that is provided is not enough to sustain circular motion then the radial distance will increase. Then the centripetal force is doing negative work, decreasing the angular velocity.

The expression for angular momentum: $m r^2 \omega$

As we know, with $\omega$ for angular velocity the expression for the conserved angular momentum is $m r^2 \omega$

While linear momentum is a property of motion along a line, angular momentum is property of motion in a plane. It can be circular motion or spiralling motion, the point is that the minimum space you need in order to have an angular momentum at all is two spatial dimensions: a plane.

As we know, when we are dealing with two spatial dimensions we are dealing with area. There is a correlation between angular momentum and area.

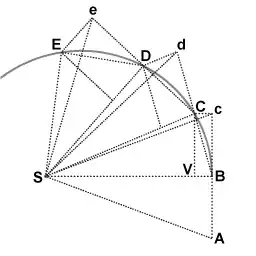
The first derivation in the Newton's Principia is a derivation of Kepler's law of areas from first principles.

(I reproduce the text from wikipedia, because I am the author of that image, and I wrote that exposition)
During the first interval of time, an object is in motion from point A to point B. Undisturbed, it would continue to point c during the second interval. When the object arrives at B, it receives an impulse directed toward point S. The impulse gives it a small added velocity toward S, such that if this were its only velocity, it would move from B to V during the second interval. By the rules of velocity composition, these two velocities add, and point C is found by construction of parallelogram BcCV. Thus the object's path is deflected by the impulse so that it arrives at point C at the end of the second interval. Because the triangles SBc and SBC have the same base SB and the same height Bc or VC, they have the same area. By symmetry, triangle SBc also has the same area as triangle SAB, therefore the object has swept out equal areas SAB and SBC in equal times.

At point C, the object receives another impulse toward S, again deflecting its path during the third interval from d to D. Thus it continues to E and beyond, the triangles SAB, SBc, SBC, SCd, SCD, SDe, SDE all having the same area. Allowing the time intervals to become ever smaller, the path ABCDE approaches indefinitely close to a continuous curve.

The above geometric reasoning shows there is a conserved quantity. This conserved quantity is proportional to the area of the triangle that are swept out. This explains why the expression for angular momentum, $m r^2 \omega$, is a quadratic expression.

Answer 2

As long as the radius stays constant, the force exerted by the rope is always perpendicular to the momentum. Therefore, only the direction of the linear momentum changes, but not its magnitude (the velocity will stay constant).

If you, however, start pulling on the rope to decrease the radius, suddenly there is an extra acceleration towards the center of the rotation. Now the force is no longer perpendicular to the direction of the velocity (to decrease the radius, the velocity vector must point slightly towards the center of the rotation). This results in an increase of the magnitude of the velocity.

Answer 3

If mass $m$ is acted on by an inward central force of magnitude F, the force is $-F \hat n$ where $\hat n$ is a unit vector radially outward. There is no force in the tangential direction even if F is changing in magnitude hence the force in the tangential direction is zero. In polar coordinates $mr \ddot \theta + 2m \dot r \dot \theta = 0$; or, equivalently, $d/dt(mr^2 \dot \theta) = 0$. $mr^2 \dot \theta$ is the angular momentum and therefore the angular momentum is constant. (The force in the outward radial direction is $-F(t) = m\ddot r - mr \dot \theta^2$.) See a good physics mechanics text, such as Mechanics by Symon.

For motion in a circle, $\dot \theta = v/r$ and the angular momentum is $mv^2/r$; if $r$ decreases $v$ increases and if $r$ increases $v$ decreases.

Answer 4

There is never any harm in going to the force diagram, as other answers have done, but if your question is "how do I develop an intuition that angular momentum should be conserved", then you can develop that based on your existing intuition that linear momentum should be conserved.

Although you probably believe it already anyway, one way to understand "why" momentum is conserved comes straight from Newton's laws, which you may or may already consider intuitive. (2) says that rate of change of momentum is proportional to force (equal if we use sensible units), and (3) says that forces come in equal-magnitude but opposite-direction pairs. That is to say, two vectors whose sum is the zero vector. So, any time a force acts, there must be two rates of change of momentum with equal magnitude and opposite direction. These cancel out in total, so total momentum is conserved.

Granted, that is not an exciting or revelatory proof mathematically, but my purpose is to establish one intuition by showing its relation to other intuitions that you already have. So, what about angular momentum?

When a force acts, consider not its magnitude and direction, but the magnitude of its component perpendicular to the line drawn from the point of action of the force, to a fixed point (usually we look at the centre of rotation as our fixed point, but in fact any other point in the universe will do for Newtonian mechanics. Einstein will make it harder, but not for 300 years). Now, everything is in motion, so that special line is moving, and I will hand-wave the difference between instantaneous forces vs. integration over time. But actually we did the same hand-wave with conservation of momentum in the case of a force that changes over time, and it didn't do us any harm.

Now, nothing has changed in Newton's laws. We still have equal and opposite forces giving us equal and opposite rates of change of momentum. But if total momentum is conserved, that means the total of any component of momentum is conserved. That's just how vector quantities work. And contact forces act at a particular point, so the distance from the fixed point to the point of action of the forces is the same for both parts of our pair of forces. And what do you get if you multiply rate of change of the perpendicular component of momentum, by distance to the centre? Rate of change of angular momentum (well, OK, actually just the rate of change of the component of angular momentum in one direction, but I'm trying to avoid vector cross products).

So, we have equal and opposite rates of change of angular momentum. Angular momentum is conserved. Hence your intuition should be that angular momentum is a "real thing", like momentum or energy, and it can't just go missing. If a spinning thing retracts towards the centre, it has to spin faster, "for the same reason that" if a moving stone gathers moss it has to move slower.

Working out the exact details of how the system achieves this conservation, then, is what the force diagram is for. But the intuition is that it has to, because otherwise there would be a violation somewhere of equal and opposite forces.

Beware also that I have ignored the case of gravity, or in fact any action at a distance. So, this intuition about how contact forces governing things on ropes must behave, unfortunately does not immediately account for situations where the two forces in our opposed pair are applied at different points.

Answer 5

A marble rolls on a spiral shaped groove. Speed of the marble does not change.

A marble moves on a circular groove, but the circle is getting bigger. Speed of the marble changes.

The difference is whether there is an inelastic collision between the marble and the groove or not.