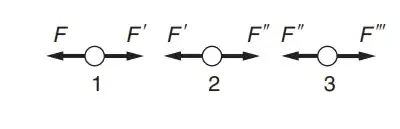
You replace your rope by a chain of $N$ rope segments (what your source calls the molecules, however that could be misleading, so stick with rope segments) with mass $m$. Each of them has the weight $F = mg$. Let's label them such that the lowest one (in a coordinate system where the vector $\textbf{g}$ points downwards) has index $1$, the second lowest index $2$ etc. In the example of the rope being fixed on a tree branch, there is no motion in the rope, so the forces on all rope segments must balance each other out.
Therefore, the lowest rope fragment experiences the downward force $F_1 = mg$ and the upward force $F_{21} = -F_1 = - mg$ (the force on segment one due to segment two). They must be the same, otherwise segment one would experience accelerating motion, which is not part of this model. Now, the second rope segment experiences $F_2 = mg + F_{12} = mg - F_{21} = 2mg$. This again must be balanced in $F_{32} = - 2mg$. Continuing this process, we find that the $k$th segment experiences a downward force $F_{k} = kmg$, which is balanced by the upward force.
This force is the tension, so we have the first result $T_k = kmg$. Now, we need to use some limiting arguments to get to a continuous description of the rope. For that, we want to send the total number $N$ of segments to infinity while keeping the total mass $M = Nm$ constant. That means we need to view $m$ as a form of density $m = M/N$. All segments should be equally spaced, so we can express $N$ by the lenght $L$ and the spacing $\Delta x$ via $N = L/\Delta x$. So the case $N \to \infty$ is tantamount to $\Delta x \to 0$.
We introduce a new variable $x = k \Delta x$ that describes at what length the index $k$ lands on the rope. Let's piece all of this together,
$$T_k = kmg = k \frac{M}{N}g = k \frac{M \Delta x}{L}g = \frac{k\Delta x}{L} Mg,$$
so in the limit $\Delta x \to 0$ with a fixed $x = k\Delta x$, we have
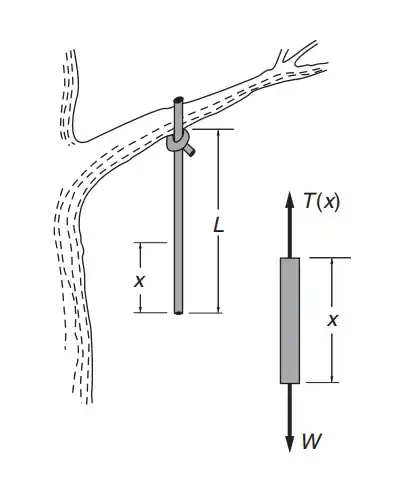
$$T(x) = \frac{x}{L} Mg.$$
Addendum
This model does not account for the dynamics of your system. The model is purely a description how a force exerted on a rope distributes over the rope in the form of a local tension (a little more precisely, we are actually dealing with a uniform force density here). I think the main confusion is because of the sort of faulty picture that identifies spring segments with molecules. This is a good description if one wanted to describe proteins, which can basically be modeled by long one-dimensional chains of molecules. A rope is usually a three-dimensional chain of molecules and it becomes kind of tricky to truly reduce this description to a molecular structure. Of course, it's not wrong to think about it this way, but then you start wondering about the motion of these molecules and all that, which isn't accounted for in this model.
The statement here is simply: You divide a rope in multiple identical segments, each of which must exert a force on its neighbor and be subject to an external force and its two neighbors' forces. You do not know how these forces relate to the stretching of the rope. All you do know is the weight $F$ on each segment, and that the rope is attached to some object (tree branch) that balances the forces and gives the rope a resulting length $L$. That (and nothing but that) is given in your model problem. You then continue, based on the model, to calculate how the force distributes over the length of the rope, giving you $T(x)$.
And that's that. The rope could be made of rubber or steel or hair. That doesn't matter in your model, as long as its final length is $L$ and its total mass is $M$, any material yields the same result. Discussion of elasticity requires a more sophisticated model, for example a chain of harmonic oscillators. Such systems can be considered when talking about linear elasticity.