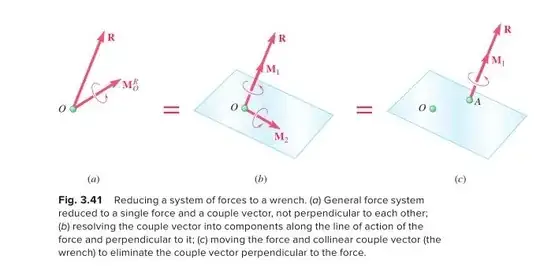
A force and couple vectors need 3+3=6 components to fully describe them.
A wrench needs 3 components for the force, 3 components for the location (one of which is ignored, as force slide along their line) and 1 component for the scalar magnitude of the parallel torque along the line. The total is 7 components, 6 of which are actually used and are entirely equivalent to the first case.
But I think the book makes the statement by disregarding the notion that the location of the force line of action is needed, and thus left for 3+1 components which is indeed less than 6.
But the simplification of a wrench has to do with the fact that coordinate transformations are eliminated from the equations of motion, or the kinematics, as it is assumed that all wrenches and twists are expressed in the same coordinate system already.
So the static equilibrium of a body is expressed with wrenches as
$$ \sum_i \hat{f}_i = \hat{0} $$
where each wrench is $\hat{f}_i = \pmatrix{ \vec{F}_i \\ \vec{r}_i \times \vec{F}_i + \vec{\tau}_i } $
This is entirely analogous to the more perceived as complex vector form
$$ \begin{aligned}
\sum_i \vec{F}_i &= \vec{0} \\
\sum_i \left( \vec{r}_i \times \vec{F}_i + \vec{\tau}_i \right) & = \vec{0}
\end{aligned} $$
So even though there isn't an actual simplification, the notation is more compact, and when I write $\sum f_i$ I immediately understand it means summing all forces and moments about the origin without having write it out explicitly every time.
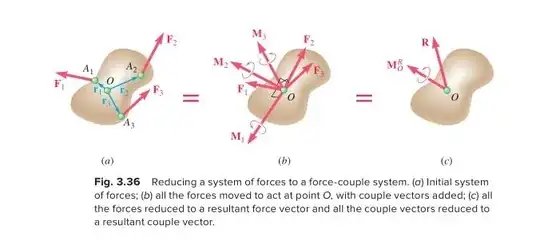
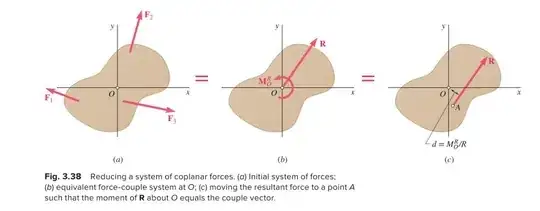 .
.