Thermal states don't have poissonian statistics.
But here @A.P. says:
If the phases of the emitted photons were uncorrelated the random interference would lead to a thermal state, as explained in this answer.
Why wouldn't randomizing the phase just force the offdiagonal elements of the coherent state density matrix to go to zero?
Let me tailor my answer for the context of your question. Let's start from the picture of a coherent classical laser beam being sent through a random phase mask:
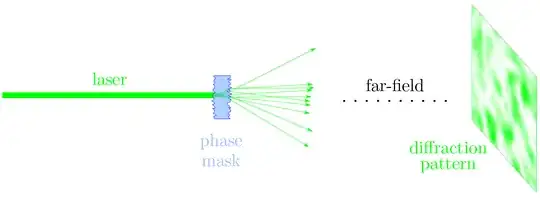
All the parts of the phase mask which are illuminated contribute light of different phase. At each point on the screen the partial beams interfere. The overall intensity at this point can be higher or lower than the average. The spread in intensities is higher than if you were to spread the laser beam over the screen with a convex lens for example. In fact, one can show that the intensity distribution on the screen is thermal. See for example Loudon – The Quantum Theory of Light chapter 3.1, especially figure 3.3 the phasor ansatz. Hence, random interference doesn't only change the off-diagonal elements in the density matrix, but changes all the statistical moments.
Now that was for a classical electric field, where it is the electric field which interferes. In the case of many phase-independent single photon emitters (the case which my answer refers to) it is the quantum paths that interfere. Quantum paths can be imagined as follows: If there are $N$ sources and $k$ detection events there are $N! / (N - k)!$ possible quantum paths that led to this result. For example source1 causes detection event1, source2 causes detection event5 and so on. Because you don't know the assignment of sources to detection events the quantum paths interfere. This leads to thermal light statistics (Bose-Einstein distribution) because of the random phases.
If there was no random interference the result would be a Binomial distribution, which in the limit $N \to \infty$ becomes a Poissonian distribution. In the case of stimulated emission the emitted photon contributes to the mode which stimulated the emission. So in the ideal case everything is in a single mode, which can't have a relative phase to itself.
Just to be clear for future people reading this question/answer. This only works for this special ``phase randomization'' described by @A.P. - in which the phase of all components of the spatial mode are assigned a random phase.
This is different from uniformly changing the phase by a random amount (which is also a common technique), which is commonly done with an EOM.
Uniform phase randomization with an EOM produces a "poisson process" (coherent state light with no offdiagonal density matrix elements). Nonuniform phase randomization (with respect to the spatial mode) produces thermal light.