1

I dont understand why the magnetic field does not curl outside the cable, according to this example, since I would expect the magnetic field lines to go back on themselves around the cable like shown in the picture and the curl would then be non-zero, right? Can someone please clarify why the curl is $0$ outside and $\neq 0$ inside?

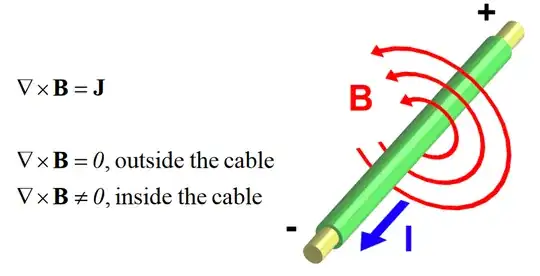
enter image description here Source of the example.

Clone
  • 285
  • 2
  • 13

3 Answers3

4

Mathematically you can surely see that $\vec{J}=0$ outside the wire and therefore the differential form of Ampere's law demands that $\nabla \times \vec{B} = 0$.

I guess what is confusing is that curl is often described in terms of "curling field lines", but that isn't entirely accurate - straight field lines can have a curl and curved field lines can have zero curl (as in this case).

A better analogy is to consider the insertion of a small paddle wheel into the problem and imagine the field lines represent a fluid flow. The question you have to ask is whether the paddle wheel will rotate.

So in this case, what would happen is the paddle wheel would not rotate because the field is curl-free. See https://physics.stackexchange.com/a/302883/43351

ProfRob
  • 141,325
2

Field lines forming closed loops does not mean the curl is non-zero at all points in space. Curl is a local property defined through derivatives, so the curl at a point just depends on the field around that point. The curl operation doesn't depend on what the field is doing elsewhere.

In this example the current density $\mathbf J$ is $0$ outside of the wire, so by $\nabla\times\mathbf B=\mathbf J$ it must be that the curl of $\mathbf B$ is $0$ outside of the wire.

BioPhysicist
  • 59,060
1

Here is a diagram of a vector field like the one you're talking about:

enter image description here

If you insert a paddle wheel ("curl meter") in this field, then the stronger field on the left compared to the right would tend to produce a clockwise torque, but the angles of the top and bottom would tend to produce a counterclockwise torque. In the actual field, the radial fall-off of the field is such that these two effects cancel, and the curl is zero.

I have a longer description of this as an example in section 11.2.1 of my book Fields and Circuits: http://lightandmatter.com/fac/

user285627
  • 11