I'm having an interpretational issue with the particles behavior around a straight cosmic string.
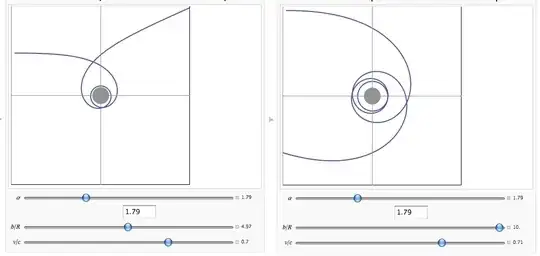
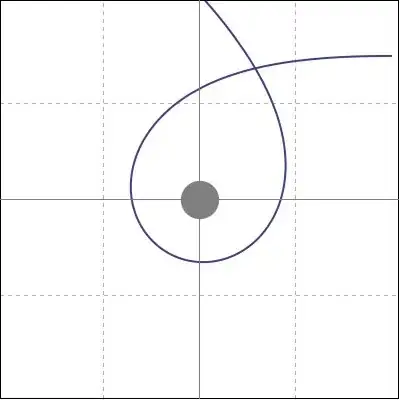
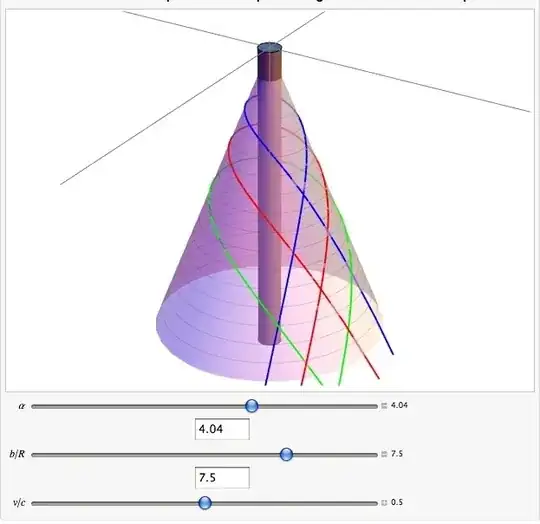
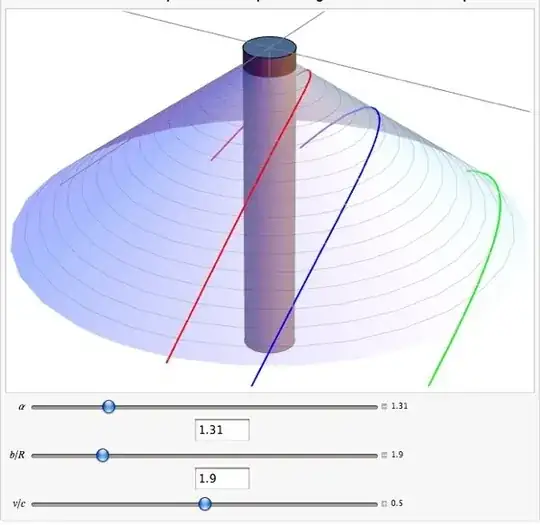
Consider the infinite cylindrical universe described by the following metric: $$\tag{1} ds^2 = dt^2 - dr^2 - (1 - 4 G \mu)^2 \, r^2 \, d\varphi^2 - dz^2. $$ To simplify things, I'll write $$\tag{2} \lambda = 1 - 4 G \mu \equiv 1 - \frac{\alpha}{2 \pi} \le 1, $$ and consider motions in the orthogonal plane only : $z = 0$ and $\dot{z} = 0$. From metric (1), it can be shown that the full Riemann curvature tensor is 0 everywhere around the string. So this spacetime is locally Minkowskian, but it has a conical topology with deficit angle $\alpha = 8 \pi G \mu$ (which gives $\lambda < 1$). I was expecting free particles to move in straight lines in this spacetime, since there's no curvature at all, and it is well known that the straight cosmic string doesn't apply any gravitational force on test-particles. Because of the deficit angle, I had a doubt so I made a numerical resolution of the geodesics equations using Mathematica. The particle's lagrangian is simply this, where the dots represent the derivative with respect to proper time $\sigma$ or an arbitrary parametrization in the case of light (when $\mathcal{L} = 0$): $$\tag{3} \mathcal{L} = \dot{t}^2 - \dot{r}^2 - \lambda^2 \, r^2 \, \dot{\varphi}^2. $$ Applying the Euler-Lagrange equations (or geodesics equation) give the following equations: \begin{align} \dot{t} \equiv \frac{d t}{d\sigma} &= \mathcal{K} = \text{constant,} \tag{4} \\[1ex] \frac{d^2 r}{d\sigma^2} &= \lambda^2 \, r \, \dot{\varphi}^2, \tag{5} \\[1ex] \dot{\varphi} \equiv \frac{d\varphi}{d\sigma} &= \frac{\mathcal{J}}{r^2}. \tag{6} \end{align} Using (6) in (5) gives $$\tag{7} \frac{d^2 r}{d\sigma^2} = \frac{\lambda^2 \mathcal{J}^2}{r^3}. $$ The constant of motion $\mathcal{J}$ is interpreted as the angular momentum of the particle, per unit mass. I then use cartesian coordinates for the numerical simulation: $x = r \cos \varphi$ and $y = r \sin \varphi$. This give the following differential equations (with $r = \sqrt{x^2 + y^2}$): \begin{align} \frac{d^2 x}{d\sigma^2} &= -\, \frac{(1 - \lambda^2) \mathcal{J}^2}{r^4} \, x, \tag{8} \\[1ex] \frac{d^2 y}{d\sigma^2} &= -\, \frac{(1 - \lambda^2) \mathcal{J}^2}{r^4} \, y. \tag{9} \end{align} So according to these equations, there's a "force" acting on the particle. Of course, it is 0 when $\lambda = 1$ (case of no deficit angle = global flat Minkowskian world). Running these equations in Mathematica gives typically the following kind of trajectories in the $x \, y$ plane (the gray disk is the cosmic string. Its radius is the unit of time and lenght. The three sliders are the deficit angle $\alpha$, the impact parameter $b$ and initial velocity $v$):
The force (8)-(9) is 0 when the particle is initially at rest (angular momentum $\mathcal{J} = 0$). This is consistent with the idea that the string doesn't apply a gravitationnal force. But from (8)-(9), there's a velocity dependant force acting on the particle, and the pictures clearly show that the string is attractive. (for some parameters, the particle could be captured by the string, and then be expulsed ...)
So how can this be, when there's no spacetime curvature at all, everywhere around the string?
Can someone point me to a freely available paper (arXiv ?) that describe these weird features of the straight cosmic string?